Представление синусоидальных величин вращающимися векторами

Для представления синусоидально изменяющейся величины , график изменения во времени, которой показан на рисунке 3.2, построим радиус-вектор этой величины 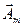, для моментов времени , t₁ - t₆. Длина этого вектора равна амплитуде синусоидальной величины . В момент времени , угол наклона вектора к горизонтальной оси равен j. В моменты времени t₁ - t₆, радиус вектор будет поворачиваться против часовой стрелки на угол . При этом его проекция на вертикальную ось будет равна 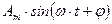. Таким образом, синусоидально изменяющуюся величину можно представить в виде вектора, вращающегося с постоянной угловой скорость w, и имеющего длину равную амплитудному значению синусоидальной величины.

Рисунок 3.2 - Представление синусоидальной величины вращающимся вектором

Применение вращающихся векторов позволяет компактно представить на одном рисунке несколько различных величин изменяющихся с одной частотой, так как их положение (угол сдвига) друг относительно друга остается неизменным. Совокупность векторов нескольких синусоидальных величин одной частоты называют векторной диаграммой. Пользуясь векторной диаграммой, сложение и вычитание мгновенных значений можно заменить сложением и вычитанием соответствующих векторов.