Представление синусоидальных величин комплексными числами

Вращающиеся векторы синусоидальных величин можно изобразить на комплексной плоскости. При этом ось абсцисс совпадает с осью действительных чисел (ось +1), а ось ординат с осью мнимых величин (+j). Любому вектору на комплексной плоскости соответствует определенное комплексное число (рисунок 3.3). Так вращающемуся вектору, синусоидальной величины , будет соответствовать комплексное число:

Рисунок 3.3 - Комплексное представление

синусоидальной величины

Комплексное число, соответствующее положению вектора в начальный момент времени (t = 0) 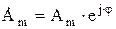- называют комплексной амплитудой синусоидальной величины. При увеличении во времени фазы синусоидальной величины угол между вектором и осью растет, функцию поворота вектора на угол относительно начального положения выполняет комплексное число . Для анализа синусоидальных величин имеющих одинаковую частоту важно взаимное положение векторов в начальный момент времени, поэтому для расчета используют только комплексные амплитуды синусоидальных величин или комплексные действующие значения. Вектор на комплексной плоскости, длина которого равна действующему значению синусоидальной величины, и соответствующее этому вектору комплексное число называют комплексным действующим значением синусоидальной величины:

Представление синусоидальной величины комплексной амплитудой или действующим значением аналогично представлению с помощью вращающегося вектора. Однако представление синусоидальных величин в комплексной форме позволяет применить эффективный комплексный метод расчета цепей синусоидального тока, то есть сложение и вычитание векторов заменить сложением и вычитанием комплексных чисел.

Применяются три формы записи комплексного значения синусоидальной величины:

- показательная форма,

- тригонометрическая форма,

- алгебраическая форма,

где 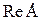и - действительная и мнимая часть комплексного значения синусоидальной величины. Переход от алгебраической формы к показательной осуществляется по формулам:

,

.

Переход от показательной формы к тригонометрической осуществляется по формуле Эйлера:

.

Сложение и вычитание комплексных величин производится в алгебраической форме, а умножение и деление в показательной. При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных величин, сокращенно их называют комплексными значениями.