
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тарау. Синусоидалық емес тоқ тізбектері
Синусоидалық емес тоқ немесе кернеу деп мәндері мен бағыты уақытқа тәуелді синусоидалық емес заңдылықпен өзгеретін тоқ пен кернеуді айтады. Электр тізбегінде синусоидалы емес тоқ немесе кернеу мына жағдайларда пайда болады:
1. Егер электр тізбегіне қосылған қоректендіргіш синусоидалы емес Э.Қ.К. өндіретін болса, онда сол тізбекте синусоидалы емес тоқ пайда болады.
2. Егер қоректендіргіш синусоидалы Э.Қ.К. өндіріп, ал ол қосылған тізбектің элементтерініңс біреуі сызықты емес болып келсе, онда ол тізбекте синусоидалы емес тоқ пайда болады.
3. Қоректендіргіш синусоидалы емес Э.Қ.К. өндіреді, ал тізбек элементтерініңс біреуі сызықты емес болып келсе, онда ол тізбекте синусоидалы емес тоқ пайда болады.
Біз периодты синусоидалы емес тоқ немесе кернеу тізбегін қарастырамыз.
а) ара тәріздес ә) тік төртбұрышты тәріздес

 i i
i i
 2
2 
 2
2 


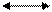 T T
T T
 б) Трапеция тәріздес в) Геометриялық дұрыс пішінді емес
б) Трапеция тәріздес в) Геометриялық дұрыс пішінді емес
 i i
i i








2  2
2 

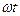
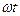
 T T
T T
Периоды 2  -ге тең кез келген синусоидалық емес шамаларды Фурье қатарына жіктеу арқылы өрнектеуге болады.
-ге тең кез келген синусоидалық емес шамаларды Фурье қатарына жіктеу арқылы өрнектеуге болады.
Жалпы жағдайда
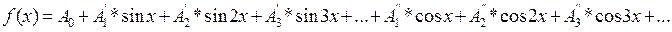 мұндағы
мұндағы 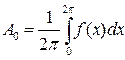 - тұрақты құрамдас бөлік;
- тұрақты құрамдас бөлік;
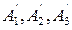 ,...-синусоида гармоникасының амплитудасы;
,...-синусоида гармоникасының амплитудасы;
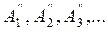 -косинусоида гармоникасының амплитудасы.
-косинусоида гармоникасының амплитудасы.
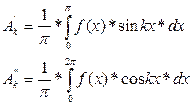
Жоғары математикадан 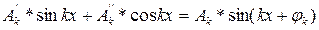
Мұндағы 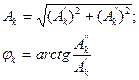
Бұл формуланы пайдаланып Фурье қатарын жазамыз:
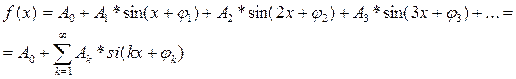
Сонымен периоды 2  -ге тең синусоидалы емес шамаларды тұрақты мүшесі бар және синусоидалық гармоникалардың жиынтығының қосындылары ретінде көрсетуге болады.
-ге тең синусоидалы емес шамаларды тұрақты мүшесі бар және синусоидалық гармоникалардың жиынтығының қосындылары ретінде көрсетуге болады.
 i
i



 am 2
am 2 
T
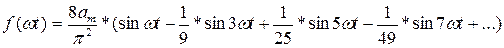
 i
i
2 



 T
T
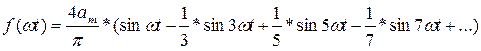
Синусоидалық емес шамаларды сипаттау үшін мынадай коэффициенттер қолданылады:
1. Амплитудалық коэффициенттері - 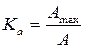 ; А - әрекеттік мән.
; А - әрекеттік мән.
2. Пішіндік коэффициенттері - 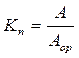
3. Бұрмалау коэффициенттері - 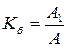 ; А1- бірінші гармониканың әрекеттік мәні.
; А1- бірінші гармониканың әрекеттік мәні.
Дата добавления: 2015-04-16; просмотров: 1298; Мы поможем в написании вашей работы!; Нарушение авторских прав |