
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Работа 7. Седиментационный анализ суспензий.
Цель работы:Определение фракционного состава и радиуса частиц фракций суспензий методом непрерывного взвешивания.
Большинство методов седиментационного анализа основано на применении закона Стокса, согласно которому сила сопротивления f движению шарообразной частицы в жидкости выражается зависимостью:
F = 6phru (7.1)
Где h - вязкость жидкости, r – радиус частиц, u – скорость движения частицы.
Если частица оседает в поле земного притяжения, то силой, вызывающей ее движение, является ее вес:
p = mg=4/3 pr3dg
где m – масса частицы, g – ускорение свободного падения; d – плотность частицы.
Потеря в весе частицы, находящейся в жидкости, по закону Архимеда составляет:
p1=4/3 pr3d1g
где d1 – плотность жидкости.
Следовательно, сила, под действием которой оседает частица в жидкой среде:
f1 = p-p1=4/3 pr3 (d-d1) g (7.2)
Вначале движение частицы происходит с ускорением. Однако при возрастании скорости движения частицы, согласно уравнению (7.1), увеличивается сопротивление среды, т.е. ускорение уменьшается и в некоторый момент времени становится равным нулю. В этот момент сила сопротивления становится равной силе, под действием которой происходит движение частицы, и далее частица движется с постоянной скоростью, которую легко найти из уравнений (7.1) и (7.2), так как:
f=f1
или
6phru=4/3 pr3 (d-d1) g
следовательно
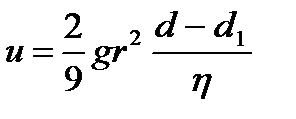 (7.3)
(7.3)
или
 (7.4)
(7.4)
Из уравнения (7.3) следует, что скорость седиментации зависит от радиуса частиц, вязкости среды и разности плотностей диспергированного вещества d и дисперсионной среды d1. В этом случае, когда плотности частиц дисперсной фазы больше плотности дисперсионной среды (d>d1), происходит седиментация частиц с образованием осадка. Наоборот, при (d<d1) диспергированное вещество всплывает на поверхность, что часто встречается при проведении дисперсионного анализа эмульсий.
Уравнение Стокса применимо при соблюдении ряда условий:
1. частицы должны быть сферическими.
Однако экспериментально показано, что уравнение Стокса применимо и для несферических частиц, поскольку отклонение в экспериментальных измерениях ввиду нешарообразной формы незначительны. Исключение составляют сильно анизодиаметричные частицы – палочкообразные или пластинчатые. Кроме того определение радиуса по уравнению (7.4) дает не действительную величину. А лишь некоторый эффективный радиус, соответствующий радиусу сферической частицы того же вещества, оседающей с той же скоростью. Такой радиус называется эквивалентным.
2. Отсутствие взаимодействия между частицами.
Взаимодействие между частицами нарушает оседание отдельных частиц и не учитывается уравнением Стокса. Однако взаимное влияние частиц при малых концентрациях суспензии, когда расстояние между частицами превышает их размеры не меньше чем в 10 раз, очень мало и не отражается на получающихся результатах. Поэтому седиментационный анализ суспензий следует проводить при небольших концентрациях (не более 1-2%).
3. Суспензия должна быть устойчивой.
В случае плохой смачиваемости частиц суспензии возможно протекание процессов коагуляции, что недопустимо. В этом случае для проведения седиментационного анализа необходимо вводить стабилизирующие или смачивающие вещества. Кроме того, оседание частиц должно происходить в спокойной жидкости при постоянной температуре.
ПРАКТИЧЕСКАЯ ЧАСТЬ.
Задание 1. Седиментационный анализ суспензии методом непрерывного взвешивания осадка.
Этот метод основан на непосредственном определении увеличения веса осадка на какой-либо поверхности при седиментации. Весовые методы высокочувствительны и позволяют анализировать суспензии малой концентрации (до 0,001%). Седиментационный анализ дисперсных систем проводят с помощью торсионных весов. В процессе измерений проводят отсчет изменений массы чашечки торсионных весов через определенные промежутки времени. По полученным данным строят кривую оседания, выражающую зависимость веса осадка р от времени седиментации t. Полученная седиментационная кривая для реальных систем обычно имеет плавный ход, и на ней укладываются все экспериментальные точки (рис. 7.1).

|
| Рис. 7.1. Седиментационная кривая |
Полная кривая седиментации получится при проведении анализа до конца, т.е. когда самые маленькие частицы осядут на чашечку микровесов. Однако часто не удается довести анализ до конца, и тогда необходимо, прежде всего, найти предел, к которому стремится кривая седиментации. Этот предел можно найти по методу Штыхнова, который состоит в том, что наряду с кривой седиментации строится кривая в координатах p, A/t, где А – любое целое число, t – время (рис. 7.1).
Участок этой кривой, соответствующий оседанию высокодисперсных фракций, оказывается приблизительно прямолинейным. Через несколько точек этого участка проводят прямую до пересечения с осью ординат. Точка пересечения а соответствует весу всего осадка, так как при t®∞, A/t®0. Прямая аb, проходящая через точку пересечения и параллельная оси абсцисс, является пределом седиментационной кривой. Этот метод нахождения предела седиментационной кривой является приближенным и рекомендуется в том случае, когда скорость оседания частиц к концу опыта очень мала и выпала большая часть частиц, а также, когда в суспензии относительно мало высокодисперсных фракций.
Разберем подробнее кривую седиментации полидисперсной суспензии. На рис. 7.2. изображен начальный участок такой кривой ОА, выражающий зависимость веса осадка от времени седиментации. В случае оседания полидисперсной суспензии, в отличие от монодисперсной, концентрация частиц на определенной глубине изменяется с течением времени. Так например, на чашечку, находящуюся на глубине h, через некоторое время от начала опыта t1 полностью осядут все частицы. Скорость оседания которых
u≥h/t1
Обозначим вес таких частиц через q. Частицы, скорость оседания которых
u<h/t1
осядут лишь частично, т.е. осядут лишь те частицы, которые в начале опыта находились от чашечки на расстоянии, меньшем чем h. Обозначим вес этих частиц через s. Вес частиц. осевших к моменту времени t1, составляет
p=q+s
и на рис. 7.2 представлен ординатой А1В1. Эквивалентный радиус частиц r1, оседающих со скоростью u=h/t1 , легко рассчитать по уравнению (7.4). Частицы большие этого радиуса также полностью осядут за время t1. Соответственно, отрезок А2В2 дает вес частиц. осевших за время t2. Отрезки прямых С1А1 и С2А2 соответствуют весу частиц. оставшихся еще в суспензии к моментам времени t1 и t2. Для определения из кривой седиментации величин q и s проведем касательную к кривой в точке А1 и продлим ее до пересечения с осью ординат. Из точки пересечения D1 проведем прямую D1E1, параллельную оси абсцисс. Скорость оседания частиц в момент времени t1 выразится производной:
dp/dt=tga
Эта производная определяет суммарную скорость седиментации фракций, частиц осевших к моменту времени t1:
dp/dt=ds1/dt+ds2/dt+…=∑dsi/dt
За период времени от 0 до t1 скорость оседания каждой из этих фракций была постоянной, соответствующей размерам частиц. Следовательно, вес частиц этих фракций, выпавших к моменту времени t1:
s=t1∑dsi/dt=t1dp/dt
Вес частиц , полностью осевших к моменту времени t1, составляет:
q= p–t1dp/dt
Из треугольника А1D1E1 очевидно, что
D1E1 = t1, A1E1 = D1E1 tga = t1 dp/dt = s
Следовательно
q = p-s = A1B1-A1E1 = E1B1 = OD1
Касательная к кривой седиментации отсекает по оси ординат отрезок, отвечающий весу частиц, осевших полностью к моменту времени, соответствующему ординате, проходящей через точку касания А1 (в данном примере t1). Если провести касательную к точке А2, то отрезок ОD2 соответствует весу частиц, полностью осевших к моменту времени t2. Из рис. 7.2 также очевидно, что отрезок OD2 – ОD1 соответствует весу фракции, содержащей частицы, оседающие со скоростью от u1 = h/t1 до u2 = h/t2, т.е. в пределах эквивалентных радиусов от r1 до r2.
Таким образом, при проведении ряда касательных к эксперимен-тально полученной кривой оседания можно разделить исследуемую полидис-персную систему на ряд фракций, размеры частиц которых лежат в некоторых пределах. Чтобы найти предельные радиусы каждой фракции, через полученные точки касания проводят ординаты, отсекающие по оси абсцисс отрезки, соответствующие времени полного оседания различных фракций. По найденным значениям t, пользуясь уравнением (7.4), вычисляют эквивалентный радиус частиц. Отрезки между касательными по оси ординат соответствуют весу отдельных фракций. Содержание в дисперсной системе отдельных фракций можно выразить в процентах от общего количества вещества. Для этого длину ординаты от 0 до предела кривой седиментации принимают за 100%. Длины отрезков, отсеченных касательными, отнесенные к общей длине ординаты, дают процентное содержание отдельных фракций в системе.

|
| Рис.7.3. Интегральные кривые. |
Результаты седиментационного анализа могут быть представлены в виде интегральной, или суммарной кривой распределения. При построении такой кривой по оси ординат откладывают процентное содержание фракций с размером частиц < r1, <r2 и т.д., а по оси абсцисс, соответственно, r1, r2 и т.д. (рис 7.3, кривая 1). Ордината каждой точки данной кривой дает процентное содержание частиц с эквивалентными радиусами, меньшими, чем соответствующий ей по оси абсцисс.
Суммарную кривую распределения можно построить и таким образом, что ордината каждой точки кривой будет давать процентное содержание частиц с большими эквивалентными радиусами, чем соответствующий ей на оси абсцисс. Для этого на оси ординат откладывают процентное содержание частиц от rmax, до rm, от rmax, до rn и т.д., а по оси абсцисс значения радиусов rm, rn и т.д.(рис. 7.3, кривая 2).
Результаты седиментационного анализа можно представить, используя функцию распределения. Допустим, что в начальный момент времени в исследуемой суспензии содержится определенное количество частиц (dQ) c эквивалентными радиусам, лежащими в пределах от r до r+dr, тогда функция распределения
f(r) = dQ/dr
а количество частиц этой фракции
dQ = f(r)dr
Относительное количество дисперсной фазы [Q(r2)–Q(r1)] с частицами, размер которых лежат в пределах от r1 до r2, можно выразить следующим соотношением:
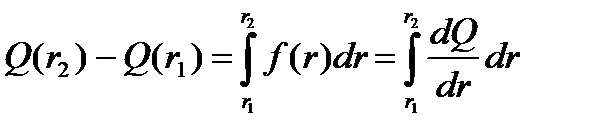

|
| Рис. 7.4. Дифференциальная кривая распределения частиц по размерам |
На рис. 7.4 представлена графически найденная зависимость. Причем по оси абсцисс нанесены значения эквивалентных радиусов, а по оси ординат f(r) = dQ/dr. Вся площадь между кривой и осью абсцисс дает общее количество частиц всех размеров, т.е. 100%, если полученные результаты анализа выражены в процентах. Процентное содержание отдельных фракций равно площади участка между ординатами соответствующих эквивалентных радиусов (от r1 до r2 на рис. 7.4).
Порядок проведения работы
Седиментационный анализ проводится при помощи торсионных весов (рис. 7.5). Прежде чем приступить к работе, устанавливают весы по уровню посредством опорных винтов 1,2. Затем освобождают коромысло весов 3 передвижением вправо арретира 4 и устанавливают стрелку-указатель 5 на 0 с помощью рычага 6. Равновесное состояние весов соответствует положению стрелки-указателя равновесия 7 против черты равновесия 8. Если при передвижении стрелки-указателя на 0 указатель равновесия не находится против черты равновесия, то его приводят к этому положению посредством винта 9. Затем, повернув арретир 4 влево. Закрепляют коромысло.
Для приготовления суспензии навеску исследуемого порошка помещают в фарфоровую ступку и перемешивают с водой, после чего переносят в стакан, который наполняют до метки дистиллированной водой[2]. Если порошок плохо смачивается жидкостью и суспензия неустойчива, то по указанию преподавателя добавляют стабилизирующие вещества. Перед опытом производят перемешивание суспензии с помощью стеклянной палочки, на конце которой прикреплен резиновый диск. Движением стеклянной палочки вверх и вниз достигают равномерного распределения частиц суспензии по всему объему. Перемешивание ведут в течение некоторого времени (3-5 мин). После окончания перемешивания суспензии ставят стакан у прибора (рис. 7.5) и быстро погружают в него чашечку, подвешивая ее на крючок коромысла 10. Одновременно с погружением чашечки включают секундомер. Освободив коромысло 3 передвижением арретира 4, замечают отклонение указателя равновесия от равновесного положения. Первый отсчет производят через 10 с. Для этого посредством рычага натяжения 6 передвигают стрелку – указатель влево до тех пор, пока указатель 7 не будет находиться против черты равновесия. По мере накопления осадка на чашечке указатель равновесия смещается влево, и во время отсчетов его возвращают снова в равновесное положение. После окончания анализа следует закрепить коромысло 3 посредством арретира 4, снять чашечку и установить стрелку-указатель 5 на 0.
Таблица 7.1
Экспериментальные данные седиментационного анализа
| № отсчета | Время отсчета | Вес чашечки с осевшими на ней частицам, мг | Вес частиц, осевших на чашечке, p, мг | Время от начала опыта t, с | 1000/t |
| 14ч 30 мин* | |||||
| 14ч 30 мин – 10с | |||||
| 14ч 30 мин – 30 с | |||||
| 14ч 30 мин – 50с |
* - время начала опыта отсчитывается от окончания перемешивания.
Скорость процесса седиментации полидисперсной суспензии бывает наибольшей в начале опыта. Поэтому в начале опыта отсчет производят через каждые 20 с; по мере приближения к концу опыта время между отсчетами постепенно увеличивают до 10-15 мин. Опыт ведут в течение 2-3ч.
Данные опыта записывают в заранее заготовленную таблицу (см. табл. 7.1).
По данным таблицы 7.1 на миллиметровой бумаге вычерчивают кривую, откладывая по оси ординат вес частиц, осевших на чашечке, p в мг, а по оси абсцисс – время от начала опыта t в с. При построении графика необходимо выбрать масштаб, удобный для дальнейшего графического расчета (рекомендуемый размер бумаги для построения седиментационных кривых – 20х40см).
Для нахождения предела седиментации по данным табл. 7.1 строят кривую в координатах p, A/t (А = 1000), подобную изображенной на рис. 7.1. К полученной седиментационной кривой проводят несколько касательных (5-7), отсекающих на оси ординат близкие по величине отрезка, и из точек касания опускают перпендикуляры на ось абсцисс.
Следует обратить внимание на определение точки касания для тех случаев, когда кривая и касательная на некотором участке полностью сливаются, т.е. когда некоторые участки кривой седиментации являются прямолинейными, что имеет место при оседании частиц с определенным радиусом. Для вычисления которого следует взять максимальное время, соответствующее точке отрыва касательной от кривой.
Ординаты, проведенные из точек касания, отсекают на оси абсцисс отрезки. Соответствующие времени полного оседания различных фракций t. По уравнению (7.4) вычисляют эквивалентные радиусы частиц, полностью осевших к моментам времени, соответствующим построенным ординатам. При вычислении эквивалентных радиусов прежде всего определяют константу уравнения (7.4):
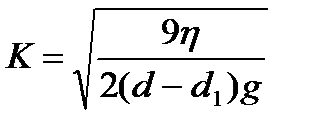
При выражении радиусов в микронах:

Скорость оседания
u=h/t
Тогда:
 , (м) (7.5)
, (м) (7.5)
Иногда для определения максимального размера частиц пользуются графическим методом: проводят касательную к начальному участку седиментационной кривой и по значению времени, соответствующему точке отрыва касательной от седиментационной кривой (tмин рис. 7.1), рассчитывают максимальный радиус по уравнению (7.5).
Следует отметить, что этот метод дает приблизительное значение rmax и его нельзя применять при анализе суспензий, содержащих небольшое количество грубых фракций.
После вычисления эквивалентных радиусов измеряют длины отрезков ординаты между касательными и выражают их в процентах от общей длины ординаты (от начала координат до предела седиментации. В табл. 7.2 ордината равна 177 мм). Отрезок ординаты от начала координат до точки пересечения первой касательной (отрезок oc на рис. 7.1), отнесенный к общей длине ординаты, дает процентное содержание частиц в интервале между максимальным эквивалентным радиусом и наибольшим, определенным по седиментационной кривой.
Из величин отдельных отрезков между касательными вычисляют процентное содержание частиц фракций между соответствующими им эквивалентными радиусами. Отрезок от предела седиментации до ближайшей к нему касательной (отрезок ad на рис. 7.1) выражает относительное содержание частиц меньше определенного из седиментационной кривой наименьшего эквивалентного радиуса (< rmin).
Таблица 7.2
Определение фракционного состава коллоидной системы.
| Время оседания t, с | Радиус частиц, r, мк | Интервалы размеров частиц отдельных фракций, мк | Длина отрезков между касательными, мм | Содержание фракций в системе, % |
| 3,9 | <3,9 | 11,9 | ||
| 3,9-5,2 | 16,4 | |||
| 5,2 | 5,2-7,7 | - | - | |
| 7,7 | - | - | - | |
| Всего….. |
Полученные на основании седиментационной кривой данные записывают в таблицу (см. табл. 7.2). На основании данных таблицы строят суммарную кривую распределения: откладывают по оси ординат суммарное процентное содержание фракций Q, начиная с наиболее мелких частиц; по оси абсцисс – радиусы частиц, соответствующие большему значению радиуса данной фракции. Например, если в исследуемом порошке наиболее мелкая фракция содержит частицы с эквивалентными радиусами < 3,9 мк и относительное количество ее в дисперсной системе 11,9%, то по оси ординат откладывают 11,9%, а по оси абсцисс – 3,9 мк; если же следующая фракция находится в пределах 3,9-5,2 мк и относительное ее количество 16,4%, то по оси ординат откладывают суммарное процентное содержание обеих фракций, т.е. 28,3%, а по оси абсцисс – 5,2 мк и т.д. Подобная суммарная кривая распределения представлена рис. 7.3 (кривая 1). Любая точка этой кривой, как указывалось ранее, показывает процентное содержание в системе частиц с меньшими эквивалентными радиусам, чем соответствующий ей по оси абсцисс. Суммарную кривую распределения можно также получить, начиная расчет от наиболее крупной фракции, причем по оси абсцисс откладывают эквивалентные радиусы, соответствующие меньшим значениям эквивалентных радиусов отдельных фракций. А по оси ординат – суммарные количества фракций в системе.
Таблица 7.3
| r | Q | DQ | DQ/Dr |
| 2,5 | |||
| 5,0 | |||
Из суммарной кривой распределения находят величины приращения процентного содержания частиц DQ через равные интервалы радиусов, для чего может быть использована любая из двух полученных кривых. Полученные данные заносят в табл. 7.3.
По данным табл. 7.3 строят дифференциальную кривую распределения (рис. 7.6), откладывая по оси ординат DQ/Dr в интервале радиусов от 0 до 2 мк равно 2,5. Графически это показано на рис. 7.6 первым прямоугольником.

|
| Рис. 7.6. Дифференциальная кривая распределения частиц по размерам. |
К построению дифференциальной кривой распределения частиц по размерам
Второй прямоугольник строят в интервале радиусов от 2 до 4 мк и т.д. – до максимального радиуса частиц. Соединив середины прямоугольников, получают плавную кривую, подобную изображенной на рис. 7.6. Максимум на дифференциальной кривой распределения соответствует наиболее вероятному размеру частиц. Форма полученной дифференциальной кривой, в зависимости от характера дисперсности исследуемой системы, может быть весьма различной.
СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА ПО РАБОТЕ
Отчет содержит название и цель работы, данные о составе исследуемых суспензий и краткое описание техники эксперимента, выводы по проделанной работе. Экспериментальные данные оформляются графически и заносятся в соответствующие таблицы.
Контрольные вопросы по работе 7.
1. Укажите, какие условия необходимо соблюдать для минимизации экспериментальных ошибок седиментационного анализа.
2. Укажите основные требования к порошкам, исследуемым методом седиментационного анализа.
Дата добавления: 2015-04-16; просмотров: 1649; Мы поможем в написании вашей работы!; Нарушение авторских прав |