Краткие теоретические сведения. При подключении конденсатора емкостью С к источнику постоянной ЭДС Е через резистор с сопротивлением R переходный процесс

При подключении конденсатора емкостью С к источнику постоянной ЭДС Е через резистор с сопротивлением R переходный процесс, как следует из второго закона Кирхгофа, описывается уравнением

R ∙ C ∙ + = E,

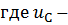мгновенное напряжение на емкости.

Решением этого уравнения является выражение

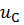= E ∙ (1 ̶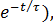

где τ = R ∙ C – постоянная времени цепи.

Если конденсатор в момент подключения к источнику постоянной ЭДС был заряжен до напряжения то напряжение на нем будет изменяться по закону

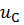= E ̶ (Е ̶ ) ∙

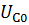Ток заряда конденсатора

i = (E ̶ u_C) / R.

Переходный процесс при разряде конденсатора на резистор согласно второму закона Кирхгофа описывается уравнением

R ∙ C ∙ 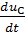+ = 0.

Решением этого уравнения является выражение

= ∙

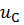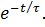
Ток разряда конденсатора

i = u_C / R.

При подключении идеальной катушки с индуктивностью L к источнику постоянной ЭДС E через резистор с сопротивлением R переходный процесс в соответствии со вторым законом Кирхгофа описывается уравнением

L ∙ + 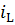∙ R = E,

где ̶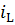 мгновенный ток через катушку.

Решение этого уравнения записывается в виде

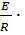= (1 ̶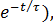

где τ = R / L – постоянная времени цепи.

Если через идеальную катушку индуктивности в момент ее подключения к источнику постоянной ЭДС протекает ток I_L0, то переходный процесс согласно второму закону Кирхгофа описывается следующим выражением

i_L = E / R – (E / R – I_L0) ∙ .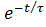

Напряжение на катушке индуктивности при подключении к ней источника ЭДС;

u_L = E – i_L ∙ R.

Переходный процесс при отключении идеальной катушки индуктивности от источника ЭДС, если до момента отключения по ней протекал ток I_L0, а ее выводы остаются присоединенными к резистору с сопротивлением R_ш, описывается уравнением

L ∙ + ∙ R_ш = 0.

Данное уравнение имеет следующее решение

= I_L0∙

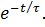
Напряжение на катушке индуктивности в данном случае

u_L = i_L ∙ R.