
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткие теоретические сведения. Переходный процесс при подключении заряженного конденсатора емкостью С к последовательно соединенной цепи из резистора c сопротивлением R и катушки c
Переходный процесс при подключении заряженного конденсатора емкостью С к последовательно соединенной цепи из резистора c сопротивлением R и катушки c индуктивностью L может быть описан с помощью следующего уравнения
L ∙ C ∙  + R ∙ C ∙
+ R ∙ C ∙  + i = 0,
+ i = 0,
где i – ток в цепи.
Если корни характеристического уравнения, полученного путем замены в данном уравнении на р обозначений производных тока цепи,
L ∙ C ∙ p2 + R ∙ C ∙ p + 1 = 0
являются комплексными сопряженными:
р1,2 = ̶ δ 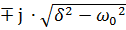 = ̶ δ
= ̶ δ  ϳ ∙
ϳ ∙  ,
,
где δ = R / (2 ∙ L) – коэффициент затухания; 
 – частота собственных колебаний;
– частота собственных колебаний;

 частота свободных колебаний,
частота свободных колебаний,
то переходный процесс будет иметь колебательный затухающий характер:
Решением уравнения, описывающего данный переходный процесс, является следующее выражение
i = ̶ 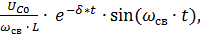
где  – начальное напряжение на конденсаторе.
– начальное напряжение на конденсаторе.
Выражение для напряжения на конденсаторе при колебательном затухающем характере переходного процесса имеет вид
uC =  sin(
sin(  ,
,
где  - начальное напряжение на конденсаторе;
- начальное напряжение на конденсаторе;
ⱷ = arctg( 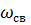 / δ).
/ δ).
Апериодический переходный процесс, происходящий при разряде конденсатора на последовательно соединенную RL-цепь, описывается тем же линейным дифференциальным уравнением второго порядка, что и колебательный затухающий. Однако оба корня его характеристического уравнения будут действительными отрицательными:
p1,2 = ̶ δ  β,
β,
где β = 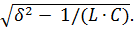
При этом решение названного дифференциального уравнения выглядит таким образом:
i = ̶ 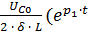 ̶
̶ 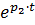 ).
).
Напряжение на конденсаторе при апериодическом характере переходного процесса изменяется по закону:
u = 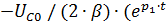 ̶
̶ 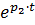 ).
).
Дата добавления: 2015-04-16; просмотров: 215; Мы поможем в написании вашей работы!; Нарушение авторских прав |