Переходные процессы в электрических цепях

Процессы перехода электрической цепи из одного установившегося состояния в другое называются переходными процессами. Они возникают в результате каких-либо переключений в цепи (коммутаций). Характер протекания переходных процессов зависит от параметров элементов цепи, схемы их соединения и начальных условий.

Рассмотрим, например, подключение простейшей цепи, состоящей из последовательно соединенных резистора с сопротивлением R и катушки с индуктивностью L, к источнику постоянной ЭДС Е (рис.3.8).

Рисунок 3.8.

Токи и напряжения в цепи установятся не сразу, т.е. будут являться функциями времени. Их называют мгновенными значениями.

Процесс в такой цепи после замыкания ключа К однозначно определяется II законом Кирхгофа, записанным для мгновенных значений, т.е. уравнением:

,

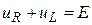где , ,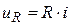

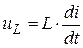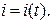
В результате подстановки получим неоднородное дифференциальное уравнение с постоянными коэффициентами:

.

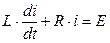Как известно, решение такого уравнения состоит из двух слагаемых:

,

где 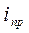– частное решения неоднородного уравнения, которое будем называть принужденной составляющей. Она равна установившемуся значению тока, т.е. току, который установится в цепи после окончания переходного процесса;

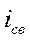– общее решения однородного уравнения (уравнения, в котором правая часть равна нулю), которое будем называть свободной составляющей.

Когда процесс в цепи установится, то в случае подключения цепи к источнику постоянной ЭДС постоянным (установившимся) будет и ток. Поэтому при i =const , получим di/dt = 0, U_L = L (di/dt) =0. Это означает, что в установившемся режиме напряжение на индуктивности равно нулю, и, следовательно, для определения составляющей i_пр можно составить расчетную модель (рис.3.9), в которой индуктивность закорочена (выброшена и заменена сопротивлением z =0). Поэтому расчет по этой модели дает:

Рисунок 3.9.

.

Для нахождения общего решения однородного уравнения 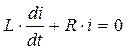нужно, как известно из математики, составить его характеристическое уравнение и найти его корни.

Получим:

,

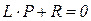откуда имеем один вещественный отрицательный корень , которому соответствует решение:

,

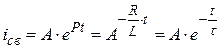где A – неизвестная постоянная интегрирования дифференциального уравнения;

– так называемая постоянная времени, измеряемая в секундах;

t – текущее время от начала коммутации (от момента включения),

измеряемое в секундах.

Складывая принужденную и свободную составляющие тока, получим:

. (3.59)

Осталось определить постоянную А. Она определяется из начальных условий.

Возникает естественный вопрос о том, что использовать в качестве известного начального условия. На интуитивном уровне понятно, что нужно использовать нечто такое, что было в цепи непосредственно до коммутации (момент t = 0_- ) и, что в момент непосредственно после коммутации (момент t = 0₊ ) не изменилось скачком, т.к. в полученном выражении (3.59) время t исчисляется от момента t = 0 = 0₊, т.е. от момента непосредственно после коммутации.

Для электрических цепей в качестве такой величины может служить энергия, запасенная в электрических и магнитных полях тех устройств, которые содержаться в цепи. Такой выбор обусловлен тем, что энергия полей не может меняться скачком.

Принимая во внимание, что энергия магнитного поля катушки индуктивности равна:

,

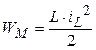получим

, .

Отсюда и получаем

,

т. е.

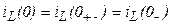(3.60)

Условие (3.60) выражает собой первый закон коммутации: ток в индуктивности не может изменяться скачком.

Поэтому, кстати, при размыкании ветвей с индуктивностью между контактами выключателя в момент включения образуется искра (электрическая дуга), поддерживающая начальное значение тока.

Аналогично можно получить второй закон коммутации: напряжение на емкости не может изменяться скачком:

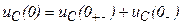(3.61)

Условия (3.60) и (3.61) называют независимыми начальными условиями, т. к. все остальные начальные условия определяются по известным независимым условиям и уравнениям Кирхгофа, составленным для цепи.

Возвращаясь к рассматриваемой задаче устанавливаем, что цепь (рис. 3.8) содержит индуктивность. Следовательно, в качестве независимого начального условия нужно использовать значения тока в индуктивности непосредственно до коммутации. До коммутации цепь была разомкнута, следовательно:

.

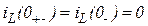В соответствие с (3.60) получаем:

.

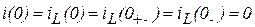Подстановка этого условия в (3.59) дает (t = 0):

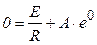, а т.к. 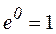, то .

Наконец, подставляя найденное значение постоянной А в (3.59), получим:

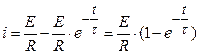(3.62)

По уравнению (3.62) можно построить график (рис. 3.10) переходного процесса для тока в цепи.

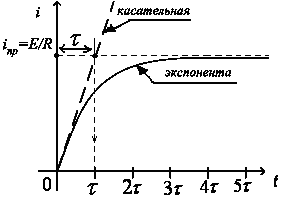
Рисунок 3.10.

Отметим, что кривая, описываемая уравнением (3.62), называется экспонентой, характерным свойством которой является то, что она теоретически бесконечно долго приближается к своему установившемуся значению . Однако, практически уже при 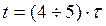ее отклонение от установившегося значения ничтожно мало. Поэтому обычно считают, что длительность переходного процесса находится в этих пределах, т.е. . А поскольку зависит, как мы установили, от параметров цепи, то и длительность переходного процесса зависит от соотношения параметров цепи. Заметим также, что, если к экспоненте из ее начала (при 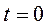) провести касательную, то на уровне установившегося значения она отсекает отрезок длиной .

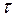Предположим, что нам нужно установить начальное значение напряжения на индуктивности. Это начальное значение является зависимым. Поэтому воспользуемся исходным уравнением, записав его для момента :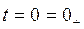

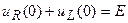, откуда

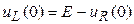, но ,

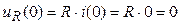поэтому .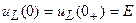

В то время, как до коммутации ( цепь отключена от источника) мы имели

, т.е. .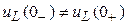

Напряжение на индуктивности меняется в момент коммутации скачком от нуля до значения ЭДС цепи.

Нетрудно и определить 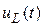, дифференцируя и умножая на 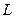уравнение (3.62):

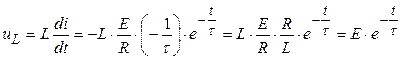.(3.63)

График, построенный по (3.63) имеет вид, представленный на рис.3.11. Напряжение на индуктивности имеет вид импульса. Из графика, кстати, видно, что , а .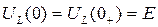

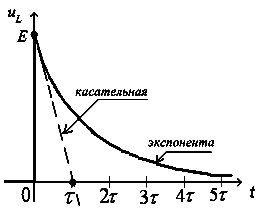
Рисунок 3.11.

Рассмотренный метод расчета называется классическим. Существует много других методов, однако, все они основаны на использовании тех идей и закономерностей, которые вошли в суть классического метода.

При этом очевидно, что при рассмотрении переходных процессов в сложных цепях решению подлежит система дифференциальных уравнений, составленных по законам Кирхгофа для мгновенных значений.

Рассмотрим в качестве примера составление системы уравнений для расчета переходного процесса в цепи, изображенной на рисунке 3.12, где e(t) – в общем случае произвольная ЭДС.

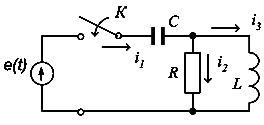
Рисунок 3.12.

Система уравнений имеет вид:

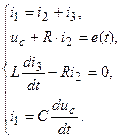
Поскольку в цепи протекает единый переходной процесс, то можно рассчитать процесс для какой-либо одной переменной, выразив все другие переменные через нее.

Выберем, например, в качестве исходной переменной напряжение на емкости u_с, тогда:

§ по (3.67) имеем ;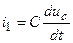

§ по (3.65) имеет ;

§ по (3.64) получим ;

§ подстановка в (3.66) дает:

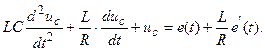. (3.68)

Решение дифференциального уравнения (3.68) позволит определить u_c(t) и затем найти все остальные переменные. Поскольку (3.68) – дифференциальное уравнение 2-го порядка, то его характеристическое уравнение всегда будет иметь два корня. При этом возможны следующие варианты:

1) корни вещественные разные р₁ и р₂:

;

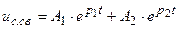2) корни вещественные кратные, т.е. р₁ = р₂ =р:

;

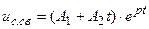3) корни комплексно-сопряженнные р_1,2 =δ 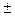jω₀:

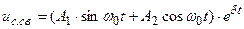
Очевидно, что при e(t) = E = const e^’(t) = 0 и тогда u_с.пр = Е, а

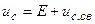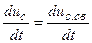, . (3.69)

Для определения двух постоянных в любом из вариантов нужно знать

u_с(0) и .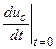

Если до коммутации конденсатор не был заряжен, то u_с(0)=u_с(0₊)=u_с(0_-)=0.

Кроме того, i_з(0) = i_з(0₊) = i_з(0_-)=0.

По (3.65) находим:

По (3.64) находим: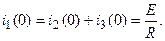

По (3.67) находим: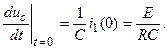

Подставляя соответствующие выражения для u_с.св (в зависимости от вида корней характеристического уравнения) для момента времени t = 0 и найденные начальные условия в уравнения (3.69), определим неизвестные постоянные интегрирования и получим решение для u_с(t), а затем по установленным связям найдем i₁(t), i₂(t), i₃(t) и, при необходимости, .

В заключение отметим, что практически все объекты электротехники, радиотехники, электроники и системотехники работают в режиме переходных процессов. Поэтому понимание их сути и подходов к анализу очень важно для современного инженера.