
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразователи координат и фаз
Математическая основа преобразования координат поясняется на рис. 3.3.

Рис.3.3 Преобразование координат.
В неподвижной системе координат (α,β) вектор тока (напряжения, потокосцепления) может быть представлен в алгебраической и показательной форме.
Аналогично в системе вращающихся координат ( x,y ) тот же самый вектор может быть представлен в виде:
 (3.9)
(3.9)
Отсюда легко получить уравнения перехода от неподвижной системы координат к вращающейся и наоборот:
 (3.10)
(3.10)
На рис. 3.4 а. представлена модель преобразователя вращающейся системы координат в неподвижную, реализованную по уравнению (3.10). На вход модели поданы проекции пространственного вектора тока на вращающиеся оси и текущее время. На выходе модели получены токи в неподвижной системе координат.. Токи видны на экране осциллоскопа. Преобразователь координат реализован в базе Subsystem, содержание которого представлено на рис. 3.4 б. Аналогичная модель строится и для преобразования переменных от неподвижной системы координат к вращающейся в соответствии с уравнениями (3.10.). Следует только заметить, что в этом случае на входе модели подаются синусоидальные функции времени, а на выходе получаются постоянные величины.


(б)
Рис.3.4 Преобразование координат convertor
При построении реальных систем электропривода переменного тока, как асинхронных, так и синхронных, практически всегда в систему управления включаются преобразователи координат. Это обусловлено тем, что реализация регуляторов возможна лишь во вращающейся системе координат, а реальные токи в обмотках статора – это токи в неподвижной системе координат.
Поэтому как правило современные электропривода переменного тока содержат преобразователи обоих типов. Кроме того они содержат преобразователи фаз 2/3 и 3/2. Первые преобразовывают токи , фазные токи, в соответствии с выражениями
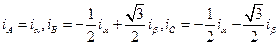 (3.11)
(3.11)
А вторые преобразовывают фазные токи в проекции, в соответствии с выражениями
 (3.12)
(3.12)
В итоге функциональная схема электропривода приобретает вид, представленный на
рис. 3.5.

Рис.3.5 Функциональная схема асинхронного электропривода.
В блоке регуляторов на основе задающего сигнала и сигналов из каналов обратной связи по переменным состояния вырабатываются сигналы управления во вращающейся системе координат, а также скорость вращения системы координат . Затем эти сигналы переводятся в систему неподвижных координат, которые направляются инвертором. Используя вращающуюся систему координат при анализе и синтезе асинхронного электропривода, удается часть схемы, обведенную жирной линией на рис. 3.5., описать одной системой уравнений . Это описание достаточно точно, когда инвертор управляется синусоидальной ШИМ. В этом случае моделирование системы не встречает больших затруднений.
Асинхронная машина с короткозамкнутым ротором.
Схема асинхронной машины с короткозамкнутым ротором (АКЗ) получается из обобщенной схемы рис 3.1., если обмотки ротора замкнуты накоротко. При этом в общих уравнениях следует положить Ur=0 .
 (3.13)
(3.13)
Для динамических систем необходимо учитывать переходные электромагнитные процессы в машине. В этом случае в качестве пары переменных, описывающих машину, оставим пространственные векторы тока статора и потокосцепления ротора, тогда уравнения (3.13) после соответствующих преобразований примут вид:
 (3.14)
(3.14)
 - безразмерные коэффициенты
- безразмерные коэффициенты
Для того чтобы лучше понять физические процессы, происходящие в АКЗ, исследуем машину в различных системах координат, сравним результаты и сделаем некоторые выводы, необходимые при построении электропривода на базе этой машины. Заметим, что для представления пространственных векторов используется комплексная плоскость.
Дата добавления: 2015-04-16; просмотров: 339; Мы поможем в написании вашей работы!; Нарушение авторских прав |