Нелинейные элементы и их характеристики. Графоаналитический метод расчета

Нелинейным элементом электрической цепи считается элемент, значения параметров которого зависят от значения тока данного элемента или напряжения на его выводах.

К нелинейным элементам электрических цепей относятся разнообразные полупроводниковые приборы, устройства, содержащие намагничивающие обмотки с ферромагнитными магнитопроводами (при переменном токе), лампы накаливания, электрическая дуга и др.

Важнейшей характеристикой нелинейных элементов является вольт-амперная характеристика (в.а.х.), представляющая собой зависимость между током нелинейного элемента и напряжением на его выводах: I(U) или U(I).

Имея в.а.х. нелинейного элемента, можно определить его сопротивления при любых значениях тока или напряжения. Различают два вида сопротивлений нелинейных элементов: статическое и дифференциальное.

Для расчета нелинейных электрических цепей применяется в большинстве случаев графоаналитический метод.

Графоаналитический метод основан на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) элементов сложной цепи.

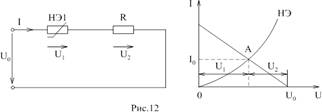Рассмотрим этот метод на примере последовательного соединения нелинейного элемента НЭ₁ и линейного R₂ (рис.12).

Характеристику нелинейного элемента I₁=f(U₁) строят обычным образом. Опрокинутая характеристика линейного элемента, представляющая собой прямую линию, может быть построена по двум точкам. Если U₂=0, то характеристике I₂=f(U₂) принадлежит точка "В", если U₁=0, то характеристика I₂=f(U₂) пересекает ось ординат в точке "С", определяемой соотношением I₂ = Uо/R. Точка пересечения двух графиков дает решение задачи.