Если , то

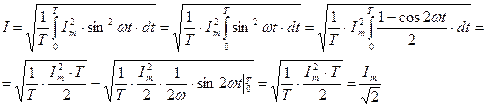
Формы представления изменяющихся электрических величин

1. График изменения во времени – волновая диаграмма
2. u(t) = U_m sin(ωt+ψ_u) - тригонометрические функции - аналитическая форма

i(t) = I_m sin(ωt+ψ_i)

1. Векторная форма

Синусоидальный ток изображен векторами, вращающимися с угловой скоростью ω, длиной амплитудного значения I_m. Для t =0 имеем вектор i­­­­­₀ = I_m sin(-ψ_i) – этот вектор - основа построения векторной диаграммы - совокупности векторов, характеризующих процессы, происходящие в цепи переменного тока, построенной с соблюдением правильной ориентации их друг относительно друга:

4. Векторная величина может быть изображена на комплексной плоскости. Вектор на плоскости, длина которого в масштабе равна действующему значению синусоидальной величины, называется комплексным действующим значением синусоидальной величины.

а и b - проекции вектора на координатные оси.

А = а + jb, а - действительная часть числа, откладывается по действительной оси абсцисс,

jb - мнимая часть числа, откладывается по оси ординат

Комплексные числа имеют 3 формы записи:

Алгебраическую: А = а + jb

Показательную: А = Аe^jα

Тригонометрическую: А = А(cos α + j·sin α)

Из рисунка:

А – модуль комплексного числа, определяется по формуле

α – аргумент, определяется по формуле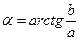

Из курса математики известна формула Эйлера: e^jα = cos α + j·sin α, следовательно A = a+jb = A·cos α +j·A·sin α = A·e^jα, где e^jα – поворотный множитель, который показывает на какой угол повернут вектор А по отношению к действительной оси. Если вместо А·e^jα взять функцию I·e^jα, то I·e^jα = I·cos α + jI·sin α – на плоскости изображается вектором e^jα величиной I, повернутым относительно оси на угол α = ωt+ ψ_i

C целью единообразия принято на комплексной плоскости изображать вектора, синусоидально изменяющиеся во времени, для момента времени ωt=0. При этом I·e^jΨ = I, где I – комплексная величина, модуль которой равен I, аргумент - угол ψ.

Примеры: 1) i = 8•sin(ωt+20) А

I_m = 8, ψ_i = 20⁰, I_m = 8·e^j20 , I =

2) I = 25e^-j30 = 25 sin(ωt-30⁰)