Замена параллельно соединенных сопротивлений одним эквивалентным.

Сопротивления соединены параллельно, если все они присоединены к одной паре узлов (рис. 1.4). Очевидно, что при этом все параллельно соединенные сопротивления находятся под одинаковым напряжением, равным напряжению источника питания.

Рис. 1.4. Параллельное соединение сопротивлений

Эквивалентное сопротивление цепи, состоящей из n параллельно соединенных сопротивлений, определяется из формулы:

.

В частном случае параллельного соединения двух сопротивлений R₁ и R₂ эквивалентное сопротивление равно

.

Преобразование треугольника сопротивлений (рис. 1.5) в эквивалентную звезду сопротивлений (рис. 1.6):

Рис. 1.5. Соединение Рис. 1.6. Соединение сопротивлений

сопротивлений треугольником звездой

; ;

; ; ,

где g – проводимость соответствующей ветви (см. рис. 1.5 и рис. 1.6).

Обратное преобразование звезды сопротивлений (рис. 1.6) в треугольник сопротивлений (рис. 1.5):

; ;

.

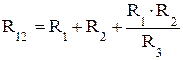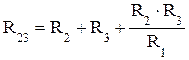Метод замены параллельно соединенных источников тока одним эквивалентным.

Если несколько источников тока с токами J₁, J₂, ..., J_n и внутренними проводимостями g₁, g₂, ..., g_n соединены параллельно (рис. 1.7), то их можно заменить одним эквивалентным источником тока, ток которого J_Э равен алгебраической сумме токов, а его внутренняя проводимость g_Э равна сумме внутренних проводимостей отдельных источников (рис. 1.8):

, .

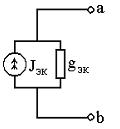
Рис. 1.7. Параллельное соединение Рис. 1.8. Эквивалентный

источников тока источник тока

1.4.7. Баланс мощностей.

Для любой замкнутой электрической цепи сумма мощностей Р_и, развиваемых источниками электрической энергии, равна сумме мощностей Р_п, расходуемых в приемниках энергии:

å Р_и=å Р_п, или å (E_kI_k + U_kJ_k)=å I²_kR_k,

где åE_kI_k – алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия э.д.с. E_k и соответствующего тока I_k совпадают, в противном случае слагаемое отрицательно; åU_kJ_k – алгебраическая сумма; здесь положительны те из слагаемых, для которых напряжение на источнике тока (оно определяется расчетом цепи внешней по отношению к зажимам источника тока) и его ток J_k совпадают по направлению, в противном случае слагаемое отрицательно; åI²_kR_k – арифметическая сумма произведений; здесь должны быть учтены как внешние сопротивления, так и сопротивления самих источников энергии.

Оба закона Кирхгофа являются следствиями закона сохранения энергии применительно к электрическим цепям.