Расчет разветвленных цепей символическим методом

Уравнения, выражающие законы Кирхгофа в комплексной форме для цепей синусоидального тока, имеют совершенно такой же вид (это было показано в предыдущих разделах), как соответствующие уравнения для цепей постоянного тока:

,

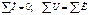только токи, напряжения, ЭДС и сопротивления входят в эти уравнения в виде комплексных величин.

Все методы расчета цепей постоянного тока получены на основе законов Кирхгофа. Если повторить все рассуждения и выводы, взяв за основу уравнения Кирхгофа в комплексной форме, то для цепей синусоидального тока можно обосновать те же методы, которые были получены для цепей постоянного тока. Несмотря на общность методов расчета цепей синусоидального и постоянного токов, расчеты цепей синусоидального тока сложнее и обладают рядом особенностей, которые будут рассмотрены в следующих разделах.

При последовательном соединении n приемников с комплексными сопротивлениями эквивалентное или общее комплексное сопротивление цепи

При параллельном соединении n приемников с комплексными проводимостями эквивалентная или общая комплексная проводимость цепи

. (3.42)

Пример смешанного соединения приемников дан на рис. 3.21.

Известно, что R₁ = 10 Ом, R₂ = 2 Ом, R₃ = 1 Ом, X_L = 1 Ом, X_C = 2 Ом.

Для данной схемы общее или эквивалентное комплексное сопротивление определяется следующим образом:

,

Переход от известного сопротивления к проводимости осуществляется по формуле

,

а переход от известной проводимости к сопротивлению

.

При преобразовании соединения потребителей треугольником в эквивалентную звезду (рис. 3.22) и обратно применяются формулы, аналогичные формулам для постоянного тока, в которых используются комплексные сопротивления и проводимости:

– преобразование «треугольник – звезда»

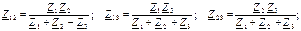(3.45)

– преобразование «звезда – треугольник»

(3.46)

Следует иметь в виду, что после преобразования соединения пассивных элементов треугольником в эквивалентное соединение звездой или обратно комплексные сопротивления преобразованной схемы могут получиться с отрицательными действительными частями, т.е. отрицательными активными сопротивлениями. Эти сопротивления имеют исключительно расчетный смысл.