
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм расчета переходного процесса классическим методом
Для анализа переходного процесса предварительно следует привести схему к минимальному числу накопителей энергии, исключив параллельные и последовательные соединения однотипных реактивных элементов (индуктивностей или емкостей). Система интегродифференциальных уравнений, составленных в соответствии с законами Кирхгофа или методом контурных токов, может быть сведена путем подстановки к одному дифференциальному уравнению, которое используется для составления характеристического уравнения.
Порядок дифференциального, следовательно, и характеристического уравнения зависит от числа реактивных элементов приведенной схемы. Главная трудность в решения задачи классическим методом для уравнений высоких порядков состоит в отыскании корней характеристического уравнения и постоянных интегрирования. Поэтому для решения уравнений порядка выше второго применяют другие методы, в частности операторный метод, основанный на применении преобразования Лапласа и исключающий трудоемкую процедуру отыскания постоянных интегрирования.
Для практических целей при анализе переходных процессов в любой схеме классическим методом может быть рекомендован следующий алгоритм.
1. Рассчитать принужденный (установившийся) режим при t→∞. Определить принужденные токи и напряжения.
2. Рассчитать режим до коммутации. Определить токи в ветвях с индуктивностью и напряжения на конденсаторах. Значения этих величин в момент коммутации является независимыми начальными условиями.
3. Составить дифференциальные уравнения для свободного процесса (Е = 0) в схеме после коммутации по законам Кирхгофа или по методу контурных токов. Алгебраизировать данные уравнения, получить характеристическое уравнение и найти его корни. Существуют приемы, упрощающие операцию отыскания корней характеристического уравнения, например, приравнивание нулю входного операторного сопротивления цепи, которое получается путем замены в выражении комплексного сопротивления цепи множителя "jω" на оператор "р".
4. Записать общие выражения для искомых напряжений и токов в соответствии с видом корней характеристического уравнения.
5. Переписать величины, полученные в п. 4, и производные от них при t = 0.
6. Определить необходимые зависимые начальные условия, используя независимые начальные условия.
7. Подставив начальные условия в уравнения п. 5, найти постоянные интегрирования.
8. Записать законы изменения искомых токов и напряжений.
Переходный процесс в цепи R, L. Установившаяся и свободная составляющие переходного процесса при включении в цепь R, L постоянной ЭДС. Определение времени завершения переходного процесса.
Рассмотрим переходные процессы в цепи, содержащей последовательно соединенные резистор R и индуктивность L . Уравнение Кирхгофа для такой цепи
 ,где u = u(t) - напряжение на входе цепи.
,где u = u(t) - напряжение на входе цепи.
Найдем решение этого уравнения для свободной составляющей тока, т.е. при u = 0, в виде iс = Iept . Для этого подставим выражение для тока в исходное уравнение и найдем значение p  .
.
Выражение Lp + R=0 представляет собой характеристическое уравнение, которое могло быть получено без подстановки общего выражения для свободной составляющей формальной заменой в однородном дифференциальном уравнении производных тока на pk, где k - порядок производной.
Таким образом, общее решение для тока при переходном процессе в R-L цепи можно представить в виде
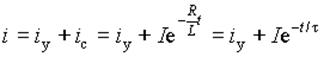 (1)
(1)
где t = 1/|p| = L/R - постоянная времени переходного процесса; I - постоянная интегрирования, определяемая по начальным значениям; i - установившийся ток в цепи, определяемый по параметрам R и L и напряжению на входе u. Длительность переходного процесса в цепи, определяемая значением t , возрастает с увеличением L и уменьшением R.
 Рассмотрим подключение R-L цепи к источнику постоянной ЭДС E (рис. 1 а)).
Рассмотрим подключение R-L цепи к источнику постоянной ЭДС E (рис. 1 а)).
Установившийся ток в этой цепи будет определяться только ЭДС E и резистивным сопротивлением R, т.к. после окончания переходного процесса i = const и uL = Ldi/dt = 0, т.е. iу = E/R .
Полный ток в переходном процессе из выражения (1)
 .
.
Для определения постоянной I найдем начальное тока. До замыкания ключа ток очевидно был нулевым, а т.к. подключаемая цепь содержит индуктивность, ток в которой не может измениться скачкообразно, то в первый момент после коммутации ток останется нулевым. Отсюда
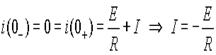 .
.
Подставляя найденное значение постоянной I в выражение для тока, получим
 . (2)
. (2)
Из этого выражения можно определить падения напряжения на резисторе uR и индуктивности uL
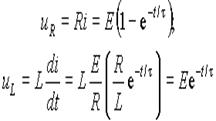 (3)
(3)
Из выражений (1)-(3) следует, что ток в цепи нарастает по экспоненте с постоянной времени t = L/R от нулевого до значения E/R (рис. 1 б)). Падение напряжения на сопротивлении uR повторяет кривую тока в измененном масштабе. Напряжение на индуктивности uL в момент коммутации скачкообразно возрастает от нуля до E , а затем снижается до нуля по экспоненте (рис. 1 б).
Подставляя выражения (3) в уравнение Кирхгофа для цепи после коммутации, можно убедиться в его справедливости в любой момент времени
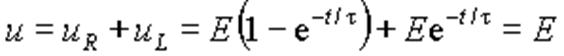 .
.
Дата добавления: 2015-04-16; просмотров: 655; Мы поможем в написании вашей работы!; Нарушение авторских прав |