Переходный процесс в цепи R, С. Установившаяся и свободная составляющие при включении в цепь R, С постоянной ЭДС. Заряд конденсатора.

Перейдем к рассмотрению переходных процессов в цепи с последовательным соединением резистора R и емкости C. По второму закону Кирхгофа для этой цепи Ri + u_C = u.

Ток в емкости можно представить в виде i = CduC/dt. Отсюда

.

Решение этого дифференциального уравнения для напряжения на емкости также можно представить суммой свободной и установившейся составляющих uC = uу + uс. Свободную составляющую найдем из решения однородного уравнения (u = 0) в виде uс = Uept. Подставим это выражение в уравнение и найдем значение p

Выражение RCp + 1 = 0 представляет собой характеристическое уравнение, которое могло быть получено без подстановки общего выражения для свободной составляющей формальной заменой в однородном дифференциальном уравнении производных от напряжения на емкости на pk, где k - порядок производной.

Отсюда общее решение для напряжения на емкости u_C = u_у + u_с= u_у + Ue- ^t/t , (8)

где U - постоянная интегрирования, определяемая из начальных значений; t = 1/|p| = RC- постоянная времени переходного процесса.

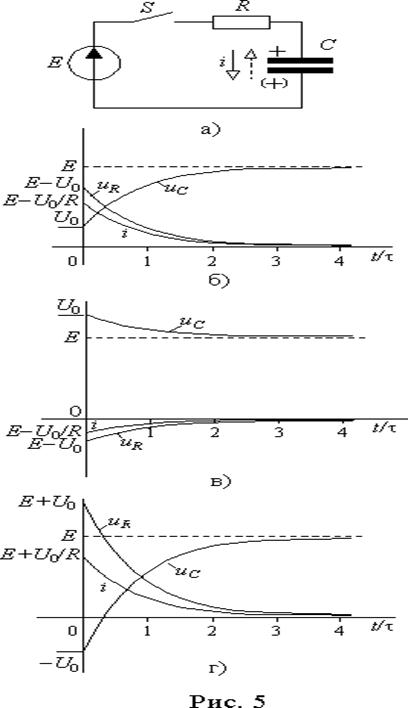
Рассмотрим процесс подключения последовательной R-C цепи к источнику постоянной ЭДС E (рис. 5 а)).

В отличие от индуктивности, емкость после накопления заряда может длительное время сохранять его. Поэтому начальное значение напряжения на емкости U0 может быть произвольным и иметь произвольный знак по отношению к ЭДС источника.

Установившееся значение напряжения на емкости после замыкания ключа S всегда будет равно E, т.к. на постоянном токе в установившемся режиме du_C/dt = 0 и i = Cdu_C/dt = 0, а u_C = u - Ri = E - Ri = E.Поэтому из выражения (8) напряжение на емкости в общем виде будет равно

u_C = u_у + u_с= E + Ue- ^t/t . (9)

Пусть напряжение на емкости до коммутации было uC(0- ) = ± U0 (знак + соответствует полярности напряжения на рис. 5 а) без скобок). Тогда из (9) для момента времени непосредственно после замыкания ключа найдем постоянную U

,

а затем и выражение для напряжения на емкости в виде

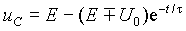(10)

где t = RC - постоянная времени переходного процесса.

Отсюда можно найти ток в цепи и падение напряжения на резисторе (11)

На рис. 5 б)-г) приведены временные диаграммы переходного процесса подключения R-C цепи к источнику постоянной ЭДС для трех вариантов начальных значений напряжения на емкости: 1) E > U0 > 0 ; 2) E < U0 и U0 > 0; 3) U0 < 0 Во всех случаях напряжение на емкости монотонно по экспоненте изменяется отU0 до E. В то время как ток и напряжение на резисторе в момент коммутации скачкообразно изменяются на величину пропорциональную разности или сумме E и U0, а затем монотонно уменьшаются до нуля. При этом, если E < U0, то ток и падение напряжения на R отрицательны, т.е. происходит разряд емкости.