Методы с использованием уравнения Кирхгофа

Рассмотрим расчёт электрической цепи, не содержащей источников тока. Рассматриваемая цепь состоит из В ветвей и У узлов. Её расчёт сводится к нахождению токов в В ветвях. Для этого необходимо составить (У - 1) независимых уравнений по первому закону Кирхгофа и К = (В - У + 1) независимых уравнений по второму закону Кирхгофа. Соответствующие этим уравнениям узлы и контуры называются независимыми (т. е. содержащими хотя бы одну ветвь, не принадлежащую другим узлам / контурам).

Для решения составленной системы уравнений можно воспользоваться матричной формой

, где

A и B — квадратные матрицы коэффициентов при токах и ЭДС порядка B x B;

I и E — матрицы-столбцы неизвестных токов и заданных ЭДС.

Решение системы:

,

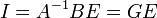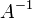
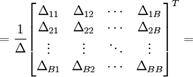
— обратная матрица; 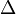— определитель матрицы A; 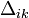— алгебраические дополнения элементов (см. способы нахождения обратной матрицы).

— матрица собственных и взаимных 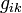проводимостей (см. метод наложения).

— система уравнений, определяющих токи ветвей.

Зачастую при расчёте цепей подобным методом возникает необходимость составления большого количества уравнений и последующего расчёта матриц большого порядка. Поэтому на практике применяются и другие методы расчёта.