Решение 1ГПЗ

Для нахождения точек пересечения прямой с поверхностью в качестве поверхности-посредника чаще всего берут проецирующую плоскость, которую проводят через данную прямую. Далее находят линию пересечения этой плоскости с поверхностью, используя 2 алгоритм, и определяют точки пересечения полученной линии с данной прямой. Эти точки и будут являться точками пересечения поверхности с прямой (рис. 3-35).

Рис. 3-35

Рассмотрим этот алгоритм на конкретном примере.

Задача: Найти точку пересечения плоскости Г(АВС) с прямой а.

Определить видимость прямой (рис. 3-36).

Рис. 3-36

Алгоритм:

1. Возьмём плоскость-посредник S так, чтобы она включала в себя прямую а и была бы проецирующей, например, относительно П₁. Тогда S₁ совпадёт с а₁ (рис. 3-37а,б).

Рис. 3-37а

Рис. 3-37б

2. Пересекаем проецирующую плоскость S с плоскостью общего положения АВС, результатом будет прямая m. Задачу решаем по 2 алгоритму: m₂ совпадает с S₂, m₁ находим по принадлежности плоскости АВС. m =12 Þ m₂ = 1₂2₂.

3. m₂, пересекаясь с а₂, даёт нам точку К₂ Þ К₁.

4. Видимость прямой а определяем методом конкурирующих точек (рис. 3-37в):

Рис. 3-37в

Видимость относительно П₂:

5ÎАВ, 3Îа - фронтально конкурирующие. На П₂ видна точка 3 Þ участок прямой а слева от точки К₂ - видимый.

Видимость относительно П₁:

2 Î ВС, 4 Î а - горизонтально конкурирующие. На П₁ видна точка 2 Þ участок прямой а справа от точки К₁ до точки 4₁ - невидимый.

Выполним краткую алгоритмическую запись решения задачи:

Г(АВС) Ç а = К. 1 ГПЗ, 3 алгоритм.

1. S - плоскость-посредник, S É а, S || П₁ Þ S₁= а₁;
2. S Ç Г = m. 2 ГПЗ, 2 алгоритм. S ^^ П₁ Þ m₁ = S₁; m₂ Ì Г
3. m₂ Ç а₂ = К₂ Þ К₁.

Такой алгоритм решения приемлем для нахождения точек пересечения любой поверхности с прямой линией. Разница заключается в форме линии m, которая является результатом пересечения плоскости-посредника с заданной поверхностью и зависит от вида поверхности. В рассмотренном примере m - это прямая линия. Если вместо плоскости Г(АВС) возьмём, например, сферу, то линия m будет являться окружностью, которая может проецироваться на какую-либо плоскость проекций в виде эллипса, если с прямой пересекается многогранник, то m - это плоский многоугольник и т.д. Подробнее рассмотрим один из таких примеров, используя указанный алгоритм решения.

Задача: Найти точки пересечения пирамиды Г(SABC) с прямой а (рис. 3-38). Определить видимость прямой.

Рис. 3-38

1. Через прямую а проведём плоскость-посредник S, проецирующую относительно П₂ (рис. 3-39а,б). S₂ = а₂.

Рис. 3-39а

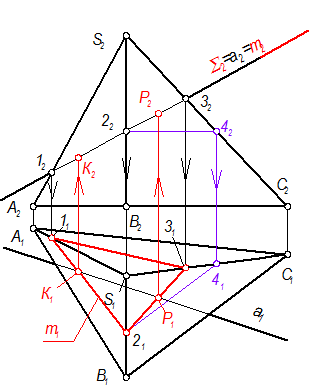
Рис. 3-39б

2. Пересекаем плоскость S с пирамидой. Результатом является замкнутая ломаная линия m(1,2,3) - треугольник. Согласно 2 алгоритму, горизонтальную проекцию треугольника строим по принадлежности пирамиде. Точки 1₁ и 3₁ находим с помощью линий связи на соответствующих рёбрах SA и SC. Точку 2₁ находим по принадлежности плоскости треугольника SBC с помощью вспомогательной прямой 24, параллельной ВС Þ 2₁4₁ || B₁C₁.

3. m₁(1₁,2₁,3₁), пересекаясь с а₁, даёт нам точки К₁ и Р₁ Þ К₂, Р₂.

4. Определяем видимость прямой на обеих проекциях (рис. 3-40). Невидимый участок прямой расположен между точками К и Р.

Рис. 3-40

Выполним алгоритмическую запись решения:

Г(SABC) Ç a = K ,P. 1 ГПЗ, 3 алгоритм.