
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение 2ГПЗ (в случае пересечения непроецирующих фигур)
Чтобы построить линию пересечения двух непроецирующих поверхностей т, нужно выполнить следующие операции:
- Задать поверхность-посредник (напоминаем, что в этом качестве чаще всего берутпроецирующую плоскость);
- Построить линии пересечения а и b поверхности-посредника с заданными поверхностями;
- Найти точки пересечения построенных линий;
- Повторять построения столько раз, сколько необходимо для того, чтобы линия пересечения поверхностей выявилась полностью;
- Определить видимость линии пересечения m и самих поверхностей.
Следует напомнить, что:
а) Решение 2 ГПЗ необходимо начинать с анализа характера пересечения поверхностей для определения количества линий пересечения m|;
б) Плоскость-посредник необходимо выбирать так, чтобы она пересекала обе поверхности по графически простым линиям - прямым или окружностям.
Рассмотрим алгоритм решения на пространственной модели (рис. 3-41):

Рис. 3-41
- Ф Ç D = m; 2ГПЗ, 3 алгоритм .
- Отмечаем очевидные точки пересечения - М и Р.
- Вводим плоскость-посредник S (как правило - проецирующую.)
- Ç Ф = а; S Ç D = b;
- а Ç b = K.
- Для построения линии m нужно найти такое количество точек, которое определяет данную линию. Для этого вводим несколько плоскостей-посредников.
- Определяем видимость линии пересечения m и поверхностей.
Задача: Построить линию пересечения конуса Ф со сферой D (рис. 3-42).
Алгоритм: 2ГПЗ , 3 алгоритм.
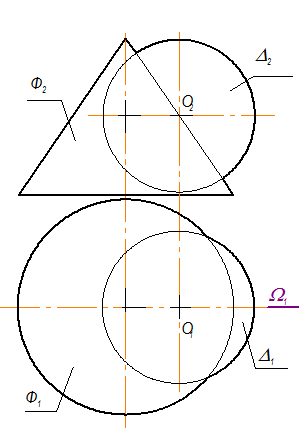
Рис. 3-42
1. Вначале определяем, что должно быть общим элементом в результате пересечения и количество общих элементов. Пересекаются две поверхности вращения второго порядка, характер пересечения - вмятие, следовательно, должна получиться одна пространственная кривая линия m. Кроме того, поверхности имеют общую плоскость симметрии (это плоскость фронтального меридиана W). Это означает, что линия пересечения симметрична относительно плоскости W, и на П2 две её ветви должны слиться в одну видимую линию.
2. Построения начинаем с характерных точек (рис.3-43), не требующих дополнительных построений для их нахождения. К ним относятся точки М и Р, лежащие в плоскости W и принадлежащие очерковым образующим конуса и сферы на П2 – М2 и P2. М1 и Р1 находим с помощью линии связи.

Рис. 3-43
3. Все остальные точки находим одинаково: задаём плоскость-посредник S (рис. 3-44). В её качестве выбираем горизонтальную плоскость уровня S2. Эта плоскость пересекает конус Ф по окружности а, радиусом R1 (от оси до очерка конуса). Проводим на П1 эту окружность а1 из центра конуса S1.

Рис. 3-44
Эта же плоскость пересекает сферу D по окружности b, радиусом R2 (от оси до очерка сферы). Проводим на П1 эту окружность b1 из центра О1 сферы.
Окружности, пересекаясь, дают нам точки К1 и К1', принадлежащие линии пересечения m. К2 и К2' находим с помощью линии связи по принадлежности плоскости S.Остальные точки находим аналогично.
4. Видимость горизонтальной проекции линии пересечения определяют точки А и А', лежащие в плоскости экватора с сферы (рис. 3-45). На П1 они принадлежат окружности с1. Все точки, расположенные ниже А2 и А2', на П1 будут невидимыми, в том числе и точки Р1, К1 и К1'.

Рис. 3-45
5. Крайние левые точки В и В' находим в плоскости S ', проходящей через точку встречи левой очерковой образующей конуса с перпендикуляром, проведённым из точки пересечения оси конуса с плоскостью экватора сферы (рис. 3-46). Построения проводим так, как описано в п.3.

Рис. 3-46
6. Конечный результат построений с учётом видимости линии пересечения и самих поверхностей приведен на рис. 3-47. Как мы и предполагали на основе анализа в п.1, линия пересечения m одна, симметрична относительно плоскости фронтального меридиана W, симметричные ветви её на П2 слились в одну видимую линию.

Рис. 3-47
Алгоритмическая запись решения:
Ф Ç D = m. 2ГПЗ, 3 алгоритм .
1. Точки М и Р Î W Þ М2; Р2 Þ М1; Р1.
2. S - плоскость-посредник; S || П1,
3. S Ç Ф = а Þ а1; S Ç D = b Þ b1; b1 Ç a1 = K1; K1' Þ K2; K2'.
4. Аналогично строим остальные точки: m1 Þ m2.
5. Видимость m относительно П1: точки А, А' Î с.
Вывод: Решение 2ГПЗ в случае пересечения непроецирующих фигур проводят по единому - третьему алгоритму и осуществляют с помощью плоскостей-посредников, которых берётся такое количество, чтобы линия пересечения выявилась полностью.
Дата добавления: 2014-11-13; просмотров: 263; Мы поможем в написании вашей работы!; Нарушение авторских прав |