Закон сохранения момента импульса.

Вывод этого закона аналогичен выводу закона сохранения импульса:

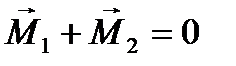Если , то

.

Обобщая, получаем

, (3.23)

где – скорость -ой массы.

Если механическая система замкнута, то центр инерции будет двигаться с постоянной скоростью ( ) поскольку в числителе (3.23) - полный импульс замкнутой системы, а он в данном случае неизменен. Ускорение центра инерции при этом равно нулю. В то же время, если система незамкнута, налицо ускорение центра инерции:

, (3.24)

где - внешняя сила, действующая на -ую массу.

Выражения (3.22), (3.23), (3.24) исчерпывающим образом характеризуют движение центра инерции.

3.5.2. Момент инерции - скалярная физическая величина, характеризующая меру инертности тела при вращательном движении. Она зависит как от массы тела, так и характера распределения массы в теле (или механической системе).

В механике различают центробежные и осевые моменты инерции (мы будем иметь дело с последними). Момент инерции тела относительно какой-то оси, например y (см. рис.3.3), определяется равенством = , (3.25)

где - момент инерции -ой материальной точки.

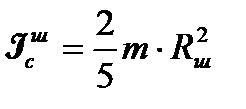В справочниках приводятся моменты инерции тел различной формы относительно оси, проходящей через их центр инерции . Например, для сплошного цилиндра , для полого цилиндра (трубы) , для шара , для стержня.

(параллелепипеда) - 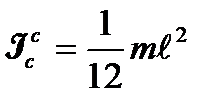, где 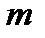- масса, R - радиус, - длина тела.

Если же ось вращения проходит не через центр инерции , то момент инерции относительно этой оси вычисляется по теореме Штейнера: , (3.26)

где - масса тела, - расстояние между данной осью 0-0 и осью, проходящей через центр инерции.

Так, для стержня массой 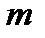и длиной , вращающегося вокруг оси, проходящей через один из его концов .