
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства лазерных пучков
Лазерное излучение характеризуется чрезвычайно высокой степенью
монохроматичности, когерентности, направленности и яркости. К этим
свойствам можно добавить пятое, а именно — малую длительность лазерных
импульсов, которая непосредственно связана с возможностями генерации
сверхкоротких импульсов света. Это свойство менее фундаментально, но тем не менее оно является весьма важным. Рассмотрим теперь перечисленные
свойства более подробно.
Монохроматичность особенно важна для процессов лазерных
измерений, локации, связи, навигации, а также лазерной химии,
разделения изотопов, медицины, биологии и т.п., кроме того, для
создания оптических систем. Она характеризуется способностью
лазеров излучать в узком диапазоне длин волн и определяется
соотношением
Mxp = Δν /ν0 (3.16)
где Δν — спектральная ширина контура излучения лазера, ν0 — центральная частота контура.
Практические значения Mxp составляют от 10–2 (эксимерный лазер) до 10–7 (He–Ne–лазер), при этом в лабораториях достигнуты значения MX ~ 10–14. Т.о., Mxp лазеров значительно превышает Mxp других спектральных источников.
На понятии монохроматичности основаны определения спектральной яркости лазеров:
 , (3.17)
, (3.17)
где Q /Δν — спектральная плотность энергии, Q — плотность энергии лазера, ΔΩ — величина телесного угла расходимости излучения. Очевидно, что спектральная яркость лазеров значительно превышает спектральную яркость всех других источников (включая Солнце) и т.п.
Когерентность.
В первом приближении, для любой электромагнитной волны можно
ввести две независимых характеристики когерентности, а именно: пространственную когерентность и временную когерентность. Для того чтобы определить понятие пространственной когерентности, рассмотрим две точки Р1 и Р2, выбранные таким образом, что в момент времени t = 0 они находятся на одном и том же волновом фронте некоторой на одном и том же волновом фронте некоторой электромагнитной волны, и пусть E1(t) и E2(t) — соответствующие напряженности электрического поля в этих точках. По определению, в момент времени t = О разность фаз напряженностей электрического поля в этих точках равна нулю. Если эта разность фаз остается равной нулю в любой момент времени t > 0, то говорят, что между этими двумя точками имеется полная когерентность. Если такая когерентность существует между любыми парами точек волнового фронта, то говорят, что данная волна характеризуется полной пространственной когерентностью. В реальности, для любой точки Р1 все точки Р2, фаза напряженности поля в которых достаточно коррелирована с фазой в точке Р1 располагаются внутри некоторой конечной области вокруг этой точки Р1. В этом случае говорят, что волна характеризуется частичной пространственной когерентностью, причем для любой точки Р можно определенным образом ввести площадь когерентности Sс(P).
Для того чтобы определить понятие временной когерентности, рассмотрим напряженности электрического поля электромагнитной волны в данной точке Р в моменты времени t и t +τ. Если при данной задержке τ разность фаз напряженностей поля остается
постоянной в любой момент времени t, то говорят о существовании временной когерентности на интервале времени τ. Если это условие сохраняется при любом значении τ, то говорят, что волна характеризуется полной временной когерентностью. Классически электромагнитной волной
с полной временной когерентностью является такая, напряженность электрического (и магнитного) поля которой может быть представлена синусоидой вида Е = E0sin (ωt + φ), где как амплитуда Е0, так и фаза φ не зависят от времени. В этом случае разность фаз в моменты времени
t и t +τ, равная Δφ = [ω(t + τ) + φ - (ωt + φ)] = ωτ, действительно не зависит от времени. Если же разность фаз напряженностей  поля остается постоянной (в среднем) при таких задержках т, что 0 < т < т0, то говорят о частичной временной когерентности волны, с характерным временем
поля остается постоянной (в среднем) при таких задержках т, что 0 < т < т0, то говорят о частичной временной когерентности волны, с характерным временем
| Рис. 5.4. Пример электромкгнитной волны с временем когерентности порядка τ0 | когерентности т0. Пример электромагнитной волны с временем когерентности, равным (примерно) т0, |
приведен на рис. 5.4. Эта волна представляет собой синусоидальное электрическое поле со скачкообразными изменениями фазы через промежутки времени т0. В этом случае при τ < τ0 разность фаз напряженностей поля остается постоянной, т.е. равной ωτ, для всех моментов времени t, кроме тех, для которых в интервале между моментами времени t и t + τ происходит скачок фазы. Напротив, если τ > τ0, то произвольный скачок фазы в интервале между моментами времени t и t + τ происходит всегда, так что получаемая разность фаз будет случайной величиной, изменяющейся в интервале от 0 до 2π.
 Можно заметить, что волна, изображенная на рис. 5.4, не является монохроматической. Действительно, если применить к соответствующему сигналу преобразование Фурье, то можно показать, что спектральная ширина этого сигнала будет составлять Δv
Можно заметить, что волна, изображенная на рис. 5.4, не является монохроматической. Действительно, если применить к соответствующему сигналу преобразование Фурье, то можно показать, что спектральная ширина этого сигнала будет составлять Δv  1 /τ0. Таким образом, по крайней мере, в рассмотренном случае, время когерентности равно τс
1 /τ0. Таким образом, по крайней мере, в рассмотренном случае, время когерентности равно τс  1 /Δv, а представление о временной когерентности, как видно, напрямую связано с понятием монороматичности.
1 /Δv, а представление о временной когерентности, как видно, напрямую связано с понятием монороматичности.
Важно отметить, что временная и пространственная когерентности не связаны друг с другом. Действительно, можно привести примеры волн с полой пространственной и только частичной временной когерентностью (и наоборот). Например, предположим, что волна,
| Рис. 5.5. Возможное поведение во времени фаз φ1(t) и φ2(t ) электромагнитных волн в двух точках Р1 и Р2, пространственная когерентность между которыми полностью отсутствует. | изображенная на рис. 5.4, представляет собой (с точностью до амплитуды) напряженность электрического поля в рассмотренных выше точках Р1 и Р2. Поскольку пространственная когерентность характеризуется разностью фаз напряженностей в двух точках в одно и то же время, то, как легко видеть, эта разность фаз |
всегда равна нулю. Таким образом, пространственная когерентность между точками Р1 и Р2 будет полной, хотя волны, проходящие через каждую из точек, имеют лишь частичную временную когерентность. В качестве второго примера допустим, что волны, проходящие через точки Р1 и Р2, имеют все тот же вид, представленный на рис. 5.4, но при этом моменты фазовых скачков и их величины абсолютно некоррелированы. Эта ситуация продемонстрирована на рис. 5.5, где построена зависимость от времени фаз φ1(t) и φ2(t) двух волн. Поскольку по-прежнему степень пространственной когерентности определяется разностью фаз напряженностей в двух точках в одно и то же время, то из рис. 5.5 нетрудно заметить, что эта разность является случайной величиной. Таким образом, имеет место полное отсутствие пространственной когерентности между двумя рассматриваемыми точками, хотя волны и характеризуются частичной временной когерентностью.
Направленность.
Это свойство является простым следствием того, что активную среду помещают в резонатор. Например, в случае плоскопараллельного резонатора, изображенного на рис. 5.3, только волны, распространяющиеся в направлении, перпендикулярном к плоскостям зеркал (или очень близком к нему), будут оставаться в резонаторе. Для более глубокого понимания свойств направленности лазерного излучения (или, в общем случае, произвольной электромагнитной волны) удобно отдельно рассмотреть случаи волн с полной и частичной пространственной когерентностью.
Рассмотрим вначале волну с полной пространственной когерентностью. Даже в этом случае пучок с конечной апертурой будет неизбежно расходиться вследствие дифракции. Эту ситуацию можно представить себе с помощью рис. 1.7, на котором изображена волна с однородным поперечным распределением интенсивности и плоским волновым фронтом, падающая на экран S с круговым отверстием диаметром D. Согласно принципу Гюйгенса волновой фронт пучка в некоторой плоскости Р за экраном можно представить как результат суперпозиции элементарных волн (вэйвлетов), испущенных из каждой точки отверстия. Видно, что из-за конечности диаметра отверстия D пучок должен иметь конечную расходимость. Для того чтобы определить величину угла дифракции 0d, рассмотрим вначале более простой случай, показанный на рис. 5.6 б, где отверстие представляет собой щель, с шириной D в плоскости рисунка и бесконечной длиной в направлении, перпендикулярном к этой плоскости. Предположим также, что щель равномерно освещена. Из рисунка нетрудно заметить, что интерференция элементарных волн, испущенных из точек в плоскости щели, приводит к нулевой интенсивности в направлении, определяемом таким углом 0, для которого выполняется условие kl = π.

Рис. 5.6.
Физическое объяснение расходимости плоской, пространственно-когерентной, электромагнитной волны вследствие дифракции (а) на экране S с круговым отверстием диаметра D, (б) на экране S с бесконечно длинной щелью шириной D
Здесь k — это постоянная распространения волны в пространстве, связанная с длиной волны излучения λ соотношением k = 2π/λ, а l — длина отрезка ВС.Действительно, в этом случае вклады в волну в направлении Θ от вэйвлетов, испущенных из точек А и B, будут противоположны по фазе и, таким образом, будут гасить друг друга. То же самое будет происходить с вэйвлетами, испущенными из точек A1 и В1 на рисунке, и т. д. Поскольку l = (D/2)sinΘ  (D/2)Θ, то, полагая, что угол дифракции пучка Θd равен углу Θ, из соотношения kl = π сразу получаем, что Θd = λ/D.
(D/2)Θ, то, полагая, что угол дифракции пучка Θd равен углу Θ, из соотношения kl = π сразу получаем, что Θd = λ/D.
В более сложных случаях величину угла Θd можно рассчитать из теории дифракции, если заданы форма отверстия и поперечное распределение интенсивности волны. Обычно получают соотношение
Θd = βλ/D, (5.16)
где множитель β — это числовой коэффициент порядка единицы, точное значение которого зависит от формы отверстия и вида распределения интенсивности излучения в его плоскости. Действительно, было показано, что в рассмотренном выше случае бесконечной щели β = 1. В качестве других примеров уместно упомянуть, что, как будет видно из последующих глав, β = 1,22 в случае равномерно освещенного кругового отверстия, тогда как β = 2/π для пучка неограниченного поперечного размера с гауссовым поперечным распределением интенсивности. Пучок, угол расходимости которого может быть выражен соотношением (5.16), в котором β  1, называют дифракционно-ограниченным.
1, называют дифракционно-ограниченным.
Если пучок имеет только частичную пространственную когерентность, то его расходимость будет больше минимальной величины, обусловленной дифракцией. Действительно, для любой точки Р' волнового фронта принцип Гюйгенса (рис. 5.6) может быть применен только к точкам, лежащим в пределах площади когерентности Sc вблизи Р'. Таким образом, размеры области когерентности играют роль ограничивающего отверстия для когерентной суперпозиции элементарных волн. В соответствии с соотношением (5.16) угол расходимости пучка можно при этом записать в виде
Θ= βλ[Sc]1/2, (5.17)
где, как и прежде, β — числовой коэффициент порядка единицы, точное значение которого зависит от того, каким образом определяются как угол расходимости Θ, так и площадь когерентности Sc.
Теперь можно показать, что поскольку волны, испущенные из каждой области когерентности, некоррелированы, т. е. некогерентны, друг с другом, на достаточно больших расстояниях (в так называемой дальней зоне)
 необходимо суммировать не напряженности, а интенсивности полей. Для того чтобы обсудить это обстоятельство, обратимся к простой ситуации, изображенной на рис. 5.7, в которой предполагается, что волна представляет собой два когерентных пучка от соседствующих источников, с диаметром поперечного сечения Dc каждый, причем эти пучки абсолютно не когерентны друг с
необходимо суммировать не напряженности, а интенсивности полей. Для того чтобы обсудить это обстоятельство, обратимся к простой ситуации, изображенной на рис. 5.7, в которой предполагается, что волна представляет собой два когерентных пучка от соседствующих источников, с диаметром поперечного сечения Dc каждый, причем эти пучки абсолютно не когерентны друг с
| Рис. 5.7. Поперечные профили пучков излучения от двух пространственно-некогерентных источников с диаметром поперечного сечения Dc на большом расстоянии L от источников | другом. Для большей определенности положим Dc = 100 мкм и λ = 1 мкм. В соответствии с соотношением (5.16) имеем Θd  10-2 рад, так что на 10-2 рад, так что на
|
расстоянии, например, L = 100 м диаметр поперечного сечения пучка,исходящего из первой области когерентности, будет равен D  Dс + 2Θd L
Dс + 2Θd L  2Θd L = 2 м. В той же плоскости диаметр поперечного сечения пучка, исходящего из второй области когерентности, будет также равен D, при этом сечения будут сдвинуты на пренебрежимо малую величину, равную Dc. Мгновенное значение интенсивности электромагнитного поля в произвольной точке Р рассматриваемой плоскости может быть представлено как I(P)α[(E1(t) +E2(t)]2, где E1(t) и E2(t) — напряженности электрических полей, наведенных в точке Р двумя областями когерентности. Полагая, что амплитуды полей постоянны во времени, перепишем это выражение в виде
2Θd L = 2 м. В той же плоскости диаметр поперечного сечения пучка, исходящего из второй области когерентности, будет также равен D, при этом сечения будут сдвинуты на пренебрежимо малую величину, равную Dc. Мгновенное значение интенсивности электромагнитного поля в произвольной точке Р рассматриваемой плоскости может быть представлено как I(P)α[(E1(t) +E2(t)]2, где E1(t) и E2(t) — напряженности электрических полей, наведенных в точке Р двумя областями когерентности. Полагая, что амплитуды полей постоянны во времени, перепишем это выражение в виде
I(P) = C[E10sin (ωt +φ1) +E20sin (ωt +φ2)]2, (5.18)
где С — некоторая константа, Е10 и Е20 — амплитуды напряженности электрических полей, а φ1 = φ1(t) и φ2 = φ2(t) — соответствующие фазы (см., например, рис. 5.5). Интенсивность, измеряемая любым реальным детектором, будет определяться величиной (1(Р)), которая представляет собой усредненную за несколько периодов колебаний интенсивность 1(Р). Тогда получаем, что эта средняя величина равна
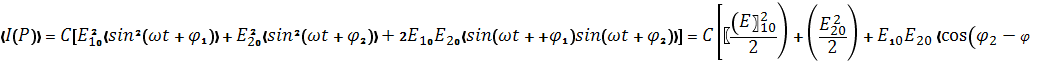 .
.
Заметим, что два фазовых члена, φ1(t) и φ2(t), могут быть представлены соответственно в виде φ1(t) = ψ1(t) +kL1 и φ2(t) =ψ2(t) + kL2 , где ψ1 и ψ2— фазы напряженностей в рассматриваемых областях когерентности, a L1 и L2 — расстояния от этих областей до точки Р. Поскольку, однако, напряженности электрического поля в двух областях когерентности некоррелированы, то фазы ψ1 и ψ2 также некоррелированы. Таким образом, разность фаз, φ2(t) – φ1(t) будет величиной, случайно изменяющейся во времени, так что среднее значение 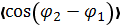 , стоящее в полученном выражении, будет равно нулю. При этом получаем:
, стоящее в полученном выражении, будет равно нулю. При этом получаем:
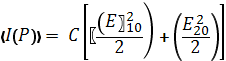 , т.е.
, т.е. 
где  – соответственно интенсивности электромагнитных волн, пришедших в точку Р из двух областей когерентности.
– соответственно интенсивности электромагнитных волн, пришедших в точку Р из двух областей когерентности.
Согласно приведенному рассмотрению, в любой точке необходимо суммировать интенсивности излучений, полученных из двух областей когерентности. Отсюда следует, что на больших расстояниях суммарный пучок будет иметь такие же поперечные размеры, что и пучок, приходящий из одной зоны когерентности.
Таким образом, имеем: D = 2ΘdL = 2β(λ/Dc)L. Следовательно, угол расходимости пучка составляет Θ = D/2L = β(λ/Dc), т. е. равен величине (5.17), если считать диаметр Dc равным квадратному корню из площади когерентности Sc.
В заключение общего описания свойств направленности электромагнитных волн следует указать, что при обеспечении определенных условий работы лазера выходящий из него пучок можно сделать полностью пространственно когерентным и, следовательно, дифракционно-ограниченным.
Яркость
Определим яркость данного источника электромагнитных волн как мощность излучения, испускаемого с единицы поверхности источника в единичный телесный угол. Точнее, рассмотрим элемент dS площади поверхности источника в точке О (рис. 5.8, а). Мощность dP, излучаемую элементом поверхности dS в телесный угол dΩ вблизи направления ОО', можно выразить в виде
dP = BcosΘdSdΩ, (5.19)
где Θ — угол между направлением ОО' и нормалью к поверхности n.Отметим, что множитель cosΘ возникает из-за того, что физически важной величиной для мощности излучения в направлении ОО' является проекция элемента dS на плоскость, перепендикулярную направлению ОО', т. е.
 cosΘdS. Величину B, определенную с помощью соотношения (5.19), называют яркостью источника в точке О в направлении ОО'. Эта величина зависит, вообще говоря, от полярных координат Θ и φ направления ОО' и от положения точки О. Если В является
cosΘdS. Величину B, определенную с помощью соотношения (5.19), называют яркостью источника в точке О в направлении ОО'. Эта величина зависит, вообще говоря, от полярных координат Θ и φ направления ОО' и от положения точки О. Если В является
| Рис. 5.8 (а) Поверхностная яркость в точке О произвольного источника электромагнитных волн, (б) Яркость лазерного пучка с диаметром D и углом расходимости Θ | постоянной величиной, то источник называют изотропным (или источником Ламберта). Рассмотрим теперь лазерный пучок мощностью Р с поперечным |
сечением в виде круга диаметром D, распространяющийся вдоль заданного направления (рис. 5.8, б). Вдоль этого направления яркость максимальна, а величина излучаемой при этом мощности определяется из соотношения (5.19), в котором cosΘ = 1. При конечных величинах площади S и телесного угла излучения Ω максимальную величину яркости можно выразить в виде В= P/SΩ. Поскольку площадь поперечного сечения пучка равна πD2/4, а телесный угол, в который происходит излучение, составляет πΘ2, где Θ — угол расходимости пучка (предполагается, что расходимость мала), то в соответствии с (5.19) для максимальной яркости пучка получаем:
 . (5.20)
. (5.20)
Отметим, что если пучок дифракционно ограничен, то Θ=Θd , и с помощью (5.16) выражение (5.20) преобразуется к соотношению
 , (5.21)
, (5.21)
которое определяет наибольшую достижимую яркость пучка мощностью Р.
Яркость является наиболее важным параметром лазерного пучка и, вообще говоря, любого источника света. Для того чтобы проиллюстрировать это утверждение, напомним вначале, что если с помощью оптической системы формируется изображение какого-либо источника света, причем и объект, и изображение находятся в одной и той же среде (например, воздухе), то справедливо следующее: яркость изображения всегда меньше или равна яркости источника, при этом равенство сохраняется только в том случае, когда в оптической системе нет потерь света, испущенного источником. Далее, предположим, что пучок на рис. 5.8, б, с углом расходимости, равным Θ, фокусируется линзой с фокусным расстоянием f. Рассчитаем интенсивность излучения в центре пятна в фокальной плоскости линзы (рис. 5.9, а). Напомним, что для проведения расчета пучок можно представить в виде непрерывного набора плоских волн с распределением углов падения на линзу порядка Θ вокруг направления распространения. Две такие волны, пересекающиеся под углом Θ', показаны непрерывной и пунктирной линиями на рис. 5.9, б. Каждая из волн фокусируется в пятно в определенном месте фокальной плоскости, и при малом угле Θ ' эти два пятна удалены на расстояние r = f Θ'. Поскольку ширина распределения углов падения

Рис. 5.9 (а) Распределение интенсивности в фокальной плоскости
линзы для пучка с углом расходимости Θ. (б) Разложение на плоские волны пучка,
изображенного в части (а)
плоских волн, образующих пучок на рис. 5.9, а, равна величине угла расходимости пучка Θ, то можно положить диаметр фокального пятна на рис. 5.9, а примерно равным d = 2fΘ. В случае идеальной непоглощающей линзы полная мощность излучения в фокальной плоскости равна мощности Р падающей волны. Таким образом, интенсивность излучения в центре пятна (пиковая интенсивность) достигает в фокальной плоскости величины Ip=4P/nd2 = P/π(f Θ)2. Переходя к яркости пучка с использованием соотношения (5.20), получаем Ip = (π/4)B(D/f)2. Видно, что Iр возрастает с увеличением диаметра пучка D. Максимальная величина Iр достигается, когда D становится равен диаметру линзы DL. При этом получаем:
Ip = π(NA)2B , (5.22)
где NA = sin[tan-1(DL/2f)]  (DL/2f)— числовая апертура линзы. Соотношение (5.22) показывает, что при заданной числовой апертуре пиковая интенсивность в фокальной плоскости линзы определяется только яркостью пучка.
(DL/2f)— числовая апертура линзы. Соотношение (5.22) показывает, что при заданной числовой апертуре пиковая интенсивность в фокальной плоскости линзы определяется только яркостью пучка.
Яркость лазера даже небольшой мощности (например, около нескольких мВт) на порядки превосходит яркость обычных источников света. Прежде всего этот факт является следствием высокой направленности лазерного пучка. В соответствии с соотношением (5.22) указанное различие означает, что пиковая интенсивность, получаемая в фокальной плоскости линзы, для лазерного пучка может быть на несколько порядков выше, чем для обычных источников света. Таким образом, интенсивность сфокусированного лазерного излучения может достигать огромных величин, что используется во многих областях применения лазеров.
Малая длительность импульсов
Не вдаваясь пока в детали, отметим, что применяя специальную технику, которая называется синхронизацией мод, оказывается возможным генерировать импульсы света, длительность которых примерно равна обратной ширине линии лазерного перехода 2 → 1. Так, длительность импульса газовых лазеров, имеющих относительно узкие линии, может достигать ~0,1-1 нс. Такие длительности не считаются достаточно малыми, и действительно, даже некоторые лампы-вспышки могут излучать импульсы длительностью менее 1 нс. С другой стороны, ширина линии у некоторых твердотельных и жидкостных лазеров может быть в 103-105 раз больше, чем у газовых лазеров; в этом случае можно получать гораздо более короткие импульсы (вплоть до ~10 фс). Это открывает потрясающие новые возможности для исследовательских и технологических применений лазеров.
Отметим, что свойство малой длительности импульса, предполагающее концентрацию энергии во времени, можно, в некотором смысле, рассматривать как противоположное монохроматичности, предполагающей концентрацию энергии в спектральном интервале. Однако это свойство, возможно, следует считать менее фундаментальным, чем монохроматичность. Действительно, тогда как в принципе достаточную монохроматичность излучения могут обеспечивать все лазеры, только лазеры с широким спектром, а именно твердотельные и жидкостные, могут генерировать импульсы сверхкороткой длительности.
Дата добавления: 2014-11-13; просмотров: 821; Мы поможем в написании вашей работы!; Нарушение авторских прав |