Уравнение движения в форме Громеки-Лэмба.

Если в (7.2) в правую часть подставить ускорение в виде (7.7) либо (7.8), то это приводит к уравнению движения в форме Громеки-Лэмба. Для установившегося движения имеем

(7.9)

Выполним некоторые преобразования (7.9).

В разделе гидростатики было введено понятие о скалярной функции , называемой силовой. Было показано, что

(7.10)

Поскольку эта функция является полным дифференциалом, то можно записать

(7.11)

Сопоставляя (7.10) и (7.11), получаем

(7.12)

С другой стороны вектор , проекциями которого являются X, Y, и Z

(7.13)

Из (7.12) и (7.13) следует, что

(7.14)

С учетом (7.14) выражение (7.9) принимает вид

(7.15)

Следует иметь в виду, что эта форма записи справедлива лишь для несжимаемой жидкости, т.е. при условии 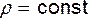. И, наконец, уравнению движения (7.15) можно придать более удобную для анализа форму, умножив скалярно его левую и правую части на произвольный направленный отрезок

(7.16)

Опуская эту операцию, которую обучающийся при желании может выполнить самостоятельно, приведем лишь конечный результат

(7.17)