Преобразование Громеки-Лэмба.

Рассмотрение теоремы Гельмгольца о движении жидкой частицы показывает, что жидкость как любое материальное тело может участвовать в поступательном и вращательном движениях.

Следует обратить внимание на то, что для совершения работы в современных технических устройствах может использоваться только энергия поступательного движения. Энергия же вращательного (вихревого) движения полностью теряется, рассеивается в окружающей среде, превращаясь в теплоту.

Система уравнений Эйлера (7.4) не учитывает факт существо­вания этих двух движений, что в определенной степени обедняет ее. Поэтому целесообразно использовать преобразование, позволяющее учесть эту особенность движения жидких частиц, называемое преобразованием Громеки-Лэмба. Формально оно сводится к тому, что в выражение для ускорения вводятся члены, характеризующие вращение жидких частиц.

Рассмотрим лишь одну компоненту:

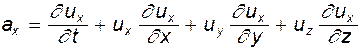(7.3)

Прибавим и вычтем в конвективной части ускорения выражение

Скомпонуем члены с учетом знаков:

Выражения в скобках есть не что иное, как удвоенные компоненты вихря и , т.е. можем записать

Подставляя полученные значения в (7.3) имеем

(7.4)

и по аналогии

(7.5)

(7.6)

В векторной форме выражение для ускорения будет иметь вид:

(7.7)

Если движение установившееся, то

(7.8)