ОСНОВЫ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ

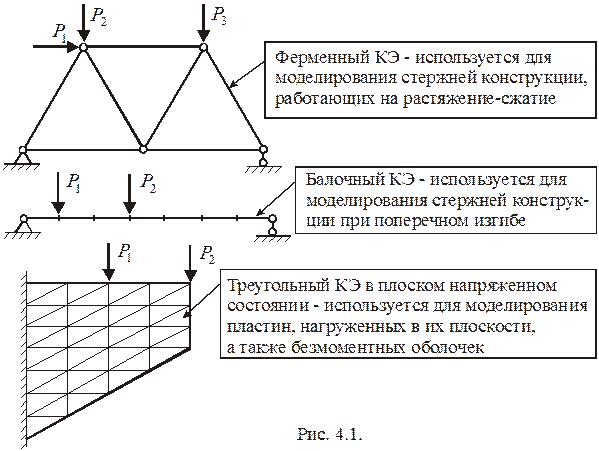
В настоящее время метод конечных элементов (МКЭ) является основным инженерным методом расчета сложных строительных, авиационных, ракетно-космических, судовых и других конструкций. Это обусловлено инвариантностью метода по отношению к геометрии конструкции, условиям ее закрепления и нагружения, а также высокой степенью приспособленности к автоматизации основных этапов расчета конструкции. С математической точки зрения МКЭ является приближенным численным методом минимизации полной потенциальной энергии упругой системы (конструкции), что имеет место в состоянии ее равновесия. В МКЭ конструкция представляется набором типовых конечных элементов. Типы используемых конечных элементов (КЭ) зависят от вида напряженного состояния конструкции и ее геометрии (рис. 4.1).

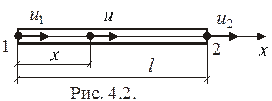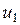Основная процедура МКЭ состоит в представлении (аппроксимации) полей перемещений конечных элементов через перемещения их узлов с помощью некоторых функций, называемых функциями распределения. Рассмотрим, к примеру, простейший КЭ - прямолинейный стержень при одноосном однородном напряженном состоянии (рис. 4.2). Перемещение произвольной точки КЭ можно выразить через узловые перемещения и 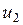так, чтобы выполнялись условия 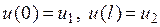: . Отсюда следуют функции распределения . Данные функции удовлетворяют условиям: в узле 1 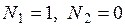; в узле 2 .

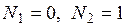Таким образом, полная потенциальная энергия конечно-элементной конструкции в конечном итоге может быть представлена как функция ее узловых перемещений 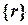. В состоянии равновесия конструкции имеет минимальное значение. Необходимое условие этого записывается в виде вариационного уравнения Лагранжа 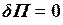(варьируемыми параметрами являются узловые перемещения 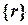), что приводит к системе линейных алгебраических уравнений

.

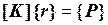Здесь 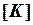, 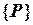- соответственно матрица жесткости и вектор внешних узловых сил (вектор нагрузки) конечно-элементной модели конструкции. Смысл полученной системы уравнений состоит в равновесии внутренних (в левой части) и внешних (в правой части) узловых сил. После определения узловых перемещений 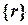находятся деформации и напряжения во всех элементах конструкции.