
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЭНЕРГИИ КОНЕЧНОГО ЭЛЕМЕНТА
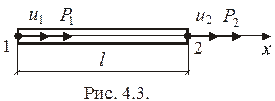 Полная потенциальная энергия
Полная потенциальная энергия 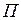 любого КЭ состоит из потенциальной энергии деформации
любого КЭ состоит из потенциальной энергии деформации 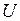 и потенциала внешних сил
и потенциала внешних сил 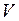 :
: 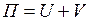 . Первое слагаемое определяется как работа обобщенных внутренних сил (напряжений) при деформировании КЭ, взятая со знаком “-“, второе слагаемое - есть работа внешних сил КЭ при переходе его из деформированного состояния в исходное (недеформированное) состояние.
. Первое слагаемое определяется как работа обобщенных внутренних сил (напряжений) при деформировании КЭ, взятая со знаком “-“, второе слагаемое - есть работа внешних сил КЭ при переходе его из деформированного состояния в исходное (недеформированное) состояние.
Рассмотрим данный вопрос на примере простейшего КЭ - прямолинейного стержня при одноосном однородном напряженном состоянии (рис. 4.3). Из курса сопротивления материалов известно, что при таком состоянии
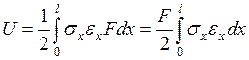 . (4.2.1)
. (4.2.1)
Здесь 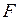 - площадь поперечного сечения КЭ, принимаемая постоянной по его длине. По закону Гука
- площадь поперечного сечения КЭ, принимаемая постоянной по его длине. По закону Гука 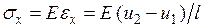 . С учетом этого выражение (4.2.1) примет вид
. С учетом этого выражение (4.2.1) примет вид
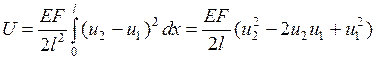 . (4.2.2)
. (4.2.2)
Из выражения (4.2.2) видно, что 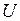 есть квадратичная форма узловых перемещений КЭ. Найдем потенциал внешних сил
есть квадратичная форма узловых перемещений КЭ. Найдем потенциал внешних сил 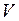 (силы приведены к узлам 1, 2 КЭ):
(силы приведены к узлам 1, 2 КЭ):  . Выражение для
. Выражение для 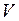 - линейная форма узловых перемещений КЭ. Полученная структура
- линейная форма узловых перемещений КЭ. Полученная структура 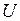 и
и 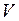 типична для всех видов конечных элементов (различие будет состоять лишь в числе узловых перемещений).
типична для всех видов конечных элементов (различие будет состоять лишь в числе узловых перемещений).
Найдем полную потенциальную энергию КЭ:
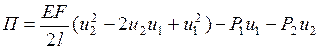 . (4.2.3)
. (4.2.3)
В состоянии равновесия КЭ
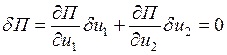 .
.
Т.к. 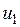 и
и 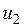 независимы, а
независимы, а 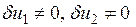 , то должны выполнятся условия
, то должны выполнятся условия
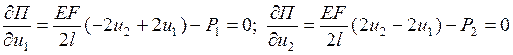 ,
,
что приводит к системе уравнений равновесия внутренних и внешних узловых сил КЭ:
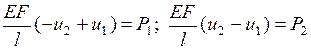 .
.
Полученную систему уравнений можно представить в матричной форме
 ,
,
где
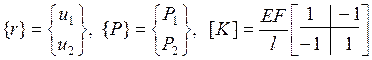
- соответственно вектор узловых перемещений, вектор нагрузки и матрица жесткости КЭ.
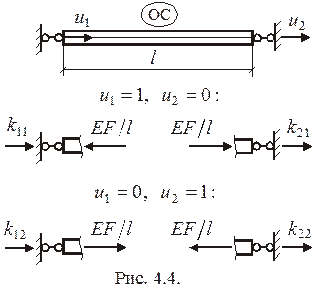 В справедливости матрицы
В справедливости матрицы  можно убедиться, определяя коэффициенты жесткости
можно убедиться, определяя коэффициенты жесткости 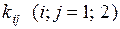 согласно их смыслу в методе перемещений:
согласно их смыслу в методе перемещений: 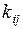 есть реакция
есть реакция 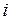 -ой дополнительной связи в основной системе (ОС) от перемещения
-ой дополнительной связи в основной системе (ОС) от перемещения 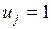 (рис. 4.4). Это дает
(рис. 4.4). Это дает
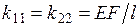 ,
,
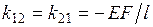 ,
,
что соответствует полученным выше результатам (см. матрицу  ).
).
После введения матриц 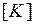 ,
, 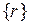 и
и 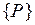 выражение (4.2.3) можно представить в матричной форме
выражение (4.2.3) можно представить в матричной форме
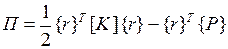 , (4.2.4)
, (4.2.4)
характерной для всех типов конечных элементов и для конструкции в целом. Нетрудно проверить, что для рассматриваемого КЭ это дает прежний результат:

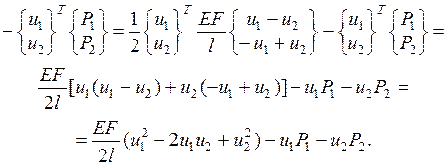
Дата добавления: 2014-11-13; просмотров: 340; Мы поможем в написании вашей работы!; Нарушение авторских прав |