УЗЛОВЫХ ПЕРЕМЕЩЕНИЙ КОНЕЧНЫХ ЭЛЕМЕНТОВ

ФЕРМЕННЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ

Узловые перемещения ферменного КЭ (рис. 4.10) в локальной и глобальной системах координат связаны соотношениями

Представляя данные соотношения в матричной форме

,

где

получаем матрицу преобразования узловых перемещений ферменного КЭ:

.

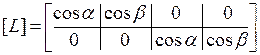Направляющие косинусы локальной оси вычисляются через глобальные координаты узлов конечного элемента:

, (4.5.1)

где - длина элемента.

БАЛОЧНЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ

Связь между узловыми перемещениями балочного КЭ (рис. 4.11) в локальной и глобальной системах координат будет такой:

Данную связь можно представить в виде:

где

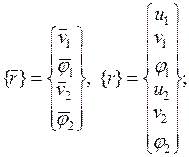
Здесь - матрица преобразования узловых перемещений балочного КЭ. Направляющие косинусы локальной оси вычисляются по формулам (4.5.1).

РАМНЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ

Перемещения узлов рамного КЭ (рис. 4.12) в локальной и глобальной системах координат связаны зависимостями

Вводя векторы

и представляя данные зависимости в виде , получаем матрицу преобразования :

Значения вычисляются по формулам (4.5.1).

ТРЕУГОЛЬНЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ ПРИ

ПЛОСКОМ НАПРЯЖЕННОМ СОСТОЯНИИ

Выберем локальную ось направленной по стороне 1-2 элемента (рис. 4.13). Вторая локальная ось 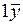располагается в плоскости элемента. Связь между перемещениями любого узла элемента в локальной и глобальной системах координат имеет вид

.

Здесь

- направляющие косинусы локальных осей .

Выражения для можно представить в матричной форме:

, (4.5.2)

где

.

Тогда связь между узловыми перемещениями и в локальной и глобальной системах координат можно представить в виде

,

где - матрица преобразования, формируемая из блоков :

.

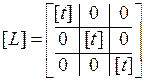Перейдем к определению направляющих косинусов, входящих в матрицу . Направляющие косинусы локальной оси определяются непосредственно через глобальные координаты узлов 1, 2:

.

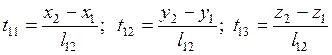Здесь - длина стороны 1-2 элемента. Для определения направляющих косинусов локальной оси 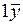введем векторы (рис. 6.4) и найдем векторное произведение:

.

Здесь

- проекции вектора на глобальные оси . Вектор согласно определению векторного произведения направлен перпендикулярно векторам так, чтобы при виде навстречу данному вектору вектор стремился поворачиваться при совмещении с вектором на наименьший угол между этими двумя векторами против хода часовой стрелки.

Далее найдем векторное произведение векторов :

,

где

Согласно прежнему определению вектор получается направленным по локальной оси 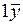. Поэтому направляющие косинусы данной оси совпадают с направляющими косинусами вектора :

,

где - длина вектора .

Локальные координаты узлов элемента, необходимые для формирования его матрицы жесткости в локальной системе координат, определяются через глобальные координаты данных узлов с использованием преобразования, аналогичного выражению (4.5.2):

.

При получаем, как и должно быть, .