КОНЕЧНЫХ ЭЛЕМЕНТОВ

После решения системы (4.7.1) с учетом условий закрепления конструкции можно определить узловые перемещения конечных элементов (они содержаться среди узловых перемещений 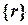конструкции). Это дает возможность определить напряженное состояние данных элементов.

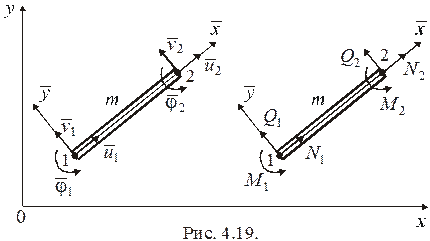
В стержневых элементах (ферменных, балочных и рамных) такое состояние определяется обобщенными внутренними узловыми силами . Положительные направления данных сил совпадают с положительными направлениями соответствующих узловых перемещений конечного элемента в локальной системе координат. Рассмотрим, к примеру, рамный элемент (рис. 4.19). Узловые перемещения элемента с некоторым номером в локальной системе координат 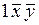и его узловые внутренние силы определяются соответственно векторами

, .

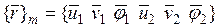Вектор определяется через вектор и матрицу жесткости элемента 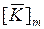в локальной системе координат:

. (4.8.1)

Выражение (4.7.1) следует непосредственно из физического смысла коэффициентов жесткости , составляющих матрицу 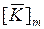: - есть внутренняя узловая сила в элементе в направлении -го перемещения от единичного -го перемещения в локальной системе координат.

Вектор определяется с использованием преобразования

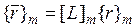, (4.8.2)

где - узловые перемещения элемента в глобальной системе координат; - матрица преобразования. С учетом данного преобразования выражение (4.8.1) примет вид

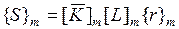. (4.8.3)

Следует заметить, что произведение уже фигурировало ранее при вычислении матрицы жесткости каждого конечного элемента в глобальной системе координат на этапе формирования матрицы жесткости 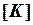конструкции, где его можно записывать на жесткий диск, а затем считывать данное произведение в цикле по элементам при определении векторов .

Напряженное состояние двумерных и трехмерных конечных элементов определяется вектором ( - номер элемента), содержащим нормальные и касательные напряжения. Рассмотрим, например, уже бывший треугольный конечный элемент, находящийся в плоском напряженном состоянии. Вектор содержит в этом случае два нормальных и одно касательное напряжение: 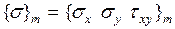. Для вычисления данного вектора через узловые перемещения элемента в глобальной системе координат воспользуемся соотношениями

. (4.8.4)

Здесь - матрица упругих свойств материала элемента; - матрица связи деформаций с узловыми перемещениями элемента в локальной системе координат; - матрица связи узловых перемещений с узловыми перемещениями . В результате получаем формулу для вычисления напряжений непосредственно через узловые перемещения конечного элемента:

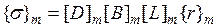. (4.8.5)

Для треугольного конечного элемента произведение вычисляется на этапе формирования полной системы уравнений и записывается на жесткий диск, а затем считывается в цикле по элементам при определении напряжений .