НАГРУЗКИ КОНЕЧНО-ЭЛЕМЕНТНОЙ МОДЕЛИ КОНСТРУКЦИИ

Узловые перемещения 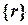конечно-элементной модели конструкции находятся из системы разрешающих уравнений 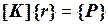. Физический смысл данной системы состоит, как известно, в равновесии внутренних и внешних узловых сил конструкции. Проследим процедуру формирования (сборки) матрицы 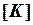на простейшем примере: прямолинейном стержне, составленном из трех ферменных конечных элементов (рис. 4.14а).

Внутренние узловые силы в конечных элементах (рис. 4.14б) определяются путем умножения матриц жесткости данных элементов на перемещения их узлов (нумерация данных сил в конечных элементах считается локальной, а нумерация узловых перемещений - глобальной):

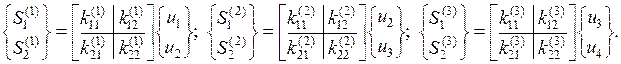
Внутренние узловые силы всего стержня составляются из узловых сил конечных элементов:

Полученные выражения можно записать в матричной форме:

.

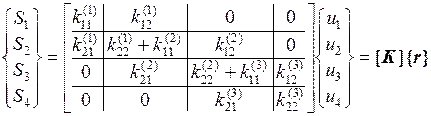Отсюда видно, что матрица жесткости 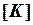всей конструкции составляется из соответствующих коэффициентов жесткости конечных элементов. При этом по направлениям перемещений, являющихся общими для смежных элементов, происходит сложение соответствующих этим перемещениям коэффициентов жесткости данных элементов. Описанная процедура формирования матрицы жесткости всей конструкции носит название метода прямой жесткости.

Аналогичным способом формируется вектор нагрузки 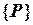конечно-элементной модели стержня из внешних узловых сил отдельных элементов:

.

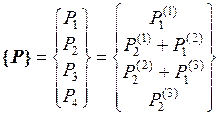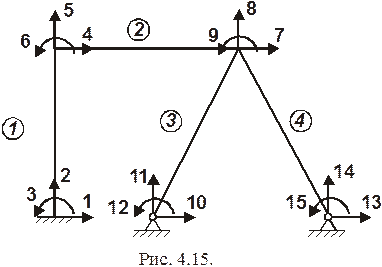
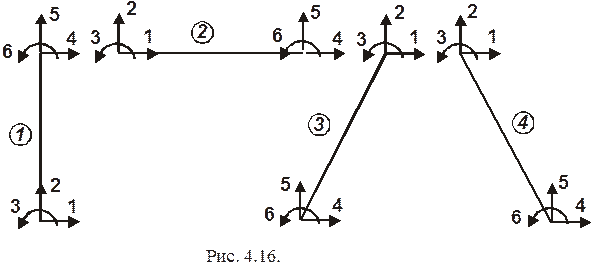
Рассмотрим плоскую раму, составленную из четырех конечных элементов (рис. 4.15). Цифрами 1, 2, 3, …,15 обозначены глобальные номера узловых перемещений конструкции, включая и нулевые перемещения, по направлениям которых имеются опорные связи (эти связи удобнее учитывать после формирования полной системы уравнений). Цифрами 1, 2, 3, 4, 5, 6 обозначены локальные номера узловых перемещений отдельных конечных элементов (рис. 4.16).

На рис. 4.17 показана схема сборки матрицы жесткости рассматриваемой рамы. Сверху и справа перечислены глобальные номера узловых перемещений конечных элементов. Значками ■, ▲, ●, ♦ на схеме условно показаны коэффициенты жесткости соответственно первого, второго, третьего и четвертого конечных элементов. Положение этих коэффициентов в матрице определяется парой глобальных индексов (глобальных номеров узловых перемещений) взамен пары соответствующих им локальных индексов. В ячейках матрицы 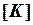, где находятся несколько значков, коэффициенты жесткости конечных элементов, соответствующие этим значкам, складываются. Пустые ячейки матрицы 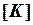содержат нули.

Аналогично формируется вектор нагрузки 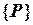всей конструкции (рис. 4.18). С целью экономии места элементы вектора 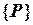расположены в массиве горизонтально. Значками ■, ▲, ●, ♦ снова показаны условно внешние узловые силы тех же конечных элементов.

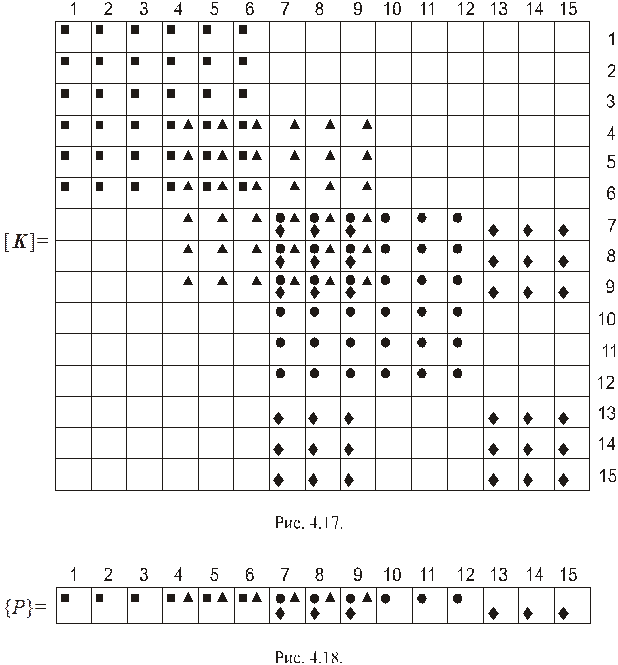
Рассмотренный выше процесс формирования матрицы жесткости 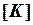и вектора нагрузки всей конструкции при большом количестве конечных элементов является весьма трудоемким и не исключает ошибок. Поэтому при расчете конструкций методом конечных элементов этот процесс осуществляется всегда автоматически. Управление сборкой матрицы и вектора 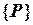производится с помощью матрицы индексов перемещений, устанавливающей соответствие между локальными и глобальными номерами узловых перемещений конечных элементов. Для рамы, показанной на рис. 4.15, матрица индексов перемещений имеет вид

.

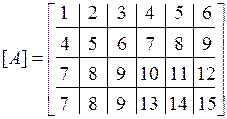В строках матрицы указаны глобальные номера узловых перемещений конечных элементов в порядке следования соответствующих им локальных номеров. Число строк в матрице равно числу конечных элементов.

Сборка матрицы 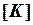и вектора 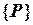осуществляется в цикле по конечным элементам. Ниже приведен фрагмент программы на языке ПАСКАЛЬ, реализующий этот процесс.

for M:=1 to NE do

begin

…….

for I:=1 to 6 do

begin

IG:=A[M,I];

P[IG]:=P[IG]+PM[I];

for J:=1 to 6 do

begin

JG:=A[M,J];

K[IG,JG]:=K[IG,JG]+KM[I,J];

end;

end;

end;

Многоточием обозначены пропущенные в цикле по конечным элементам операции, необходимые для формирования матрицы жесткости и вектора нагрузки текущего элемента. Обозначения в программе:

· М – номер текущего конечного элемента;

· NE – число конечных элементов;

· A – матрица индексов перемещений;

· I, J – локальные индексы узловых перемещений конечного элемента;

· IG, JG – соответствующие им глобальные индексы, выбираемые из матрицы A;

· K, P – соответственно матрица жесткости и вектор нагрузки конструкции;

· KM, PM – соответственно матрица жесткости и вектор нагрузки текущего конечного элемента с номером M.

После завершения цикла по конечным элементам к вектору нагрузки 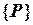добавляются еще сосредоточенные силы и моменты по направлениям соответствующих им узловых перемещений.