Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.

Очевидно, что вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.

Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым.

Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.

Тогда в соответствием с записанными выше формулами получаем:

Отметим, что вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий.

Определение. Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов.

Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.

Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна:

Как видно, эта величина не совпадает с найденной вероятностью.

При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события.

Вообще говоря, классическое определение вероятности – довольно относительное.

Это обусловлено тем, что на практике сложно представить результат опыта в виде совокупности элементарных событий, доказать, что события равновероятные.

К примеру, при произведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т.д.

Классическое определение вероятности неприменимо к испытаниям с бесконечным числом исходов. Чтобы преодолеть этот недостаток вводится понятие геометрической вероятности, т.е. вероятности попадания точки в какой – либо отрезок или часть плоскости (пространства).

Так если на отрезке длиной L выделен отрезок длины l, то вероятность попадания наугад взятой точки в отрезок l равна отношению l/L.

2. Операции над событиями

Определение. События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.

Определение. Объединениемили суммой событий А_к называется событие A, которое означает появление хотя бы одногоиз событий А_к.

Определение. Пересечениемили произведениемсобытий A_k называется событие А, которое заключается в осуществлении всех событий A_k.

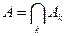
Определение. Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.

Определение. Дополнительным к событию А называется событие , означающее, что событие А не происходит.

Определение. Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.

Совокупность всех элементарных исходов опыта называется пространством элементарных событий.

Тестовые вопросы для самоконтроля:

1. Испытание это:

а) событие

б) определенный комплекс условий, в котором наблюдается то или иное явление; фиксируется тот или иной результат.

в) происшествие

2. Событие это:

а) испытание б) происшествие

в) факт, который в результате опыта может произойти или не произойти.

3. Вероятность события это:

а) численная мера степени наступления события.

б) численная мера степени наступления испытания.

в) элементарный исход.

4.Являются ли несовместными следующие события:

а) опыт – бросание монеты; события:

А - появление герба, В - появление реверса

б) опыт – бросание двух монет; события:

С - появление герба на первой монете

Д - появление реверса на второй монете

в) опыт – два выстрела по мишени; события:

Е - хотя бы одно попадание,

F - хотя бы один промах

5. Являются ли равновозможными следующие события:

а) опыт – бросание монеты; события:

А – появление герба, В - появление цифры

б) опыт – бросание двух монет; события:

С - появление двух гербов, Д – появление двух цифр

в) опыт – бросание игральной кости; события:

Е – появление трех очков ,

Д – появление менее трех очков.

6. Образуют ли полную группу следующие группы событий:

а) опыт – бросание двух монет; события

А – появление двух гербов, В - появление двух цифр

б) опыт – бросание монеты; события:

С – появление герба, Д – появление цифры

в) опыт – извлечение карты из колоды; события:

Е – появление карты червовой масти;

F - появление карты бубновой масти;

К - появление карты трефовой масти;

7. Статистическая вероятность это

а) вероятность случайного события

б) геометрическая вероятность

в) относительная частота появления события.

8. Формула нахождения события согласно классическому определению вероятности события

а) Р(А)= 1 б) Р (А)= в) W (A)=

9. Вероятность попадания точки на часть плоскости можно найти по формуле нахождения

а) статистической вероятности

б) вероятности невозможно события.

в) геометрической вероятности

10. Сколькими способами можно расставить 5 самоваров на витрине магазина?

а) 25 б) 5 в) 120

Рекомендуемая литература

Основная:

1. Общий курс высшей математики для экономистов [Текст]: Учебник /Под ред. В. И. Ермакова.- М.: Инфра-М, 2008.- 656 с.- Гриф МО

2. Тырсин, А. Н. Математика.Теория вероятностей и математическая статистика [Текст] : учебное пособие/ А. Н. Тырсин.- Челябинск: Челяб. гос. ун-т, 2007.- 235 c.

Дополнительная:

1. Сборник задач по высшей математике для экономистов [Текст]: Учебное пособие.- 2-е изд., испр.- М.: Инфра-М, 2008.- 574 с.- Гриф УМО