
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Среднее квадратическое отклонение
Определение. Средним квадратическим отклонениемслучайной величины Х называется квадратный корень из дисперсии.


Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.

Пример. Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта. Наугад выбирают 1000 изделий. Пусть Х – число изделий первого сорта в данной выборке. Найти закон распределения, математическое ожидание и дисперсию случайной величины Х.
Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна р = 0,96.
Таким образом, закон распределения может считаться биноминальным.


Пример. Найти дисперсию дискретной случайной величины Х – числа появлений события А в двух независимых испытаниях, если вероятности появления этого события в каждом испытании равны и известно, что М(Х) = 0,9.
Т.к. случайная величина Х распределена по биноминальному закону, то

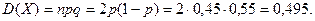
Пример. Производятся независимые испытания с одинаковой вероятностью появления события А в каждом испытании. Найти вероятность появления события А, если дисперсия числа появлений события в трех независимых испытаниях равна 0,63.
По формуле дисперсии биноминального закона получаем:




Пример. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно р1=0,3; p2=0,4; p3=0,5; p4=0,6. Найти математическое ожидание и дисперсию числа отказавших приборов.
Принимая за случайную величину число отказавших приборов, видим, что эта случайная величина может принимать значения 0, 1, 2, 3 или 4.
Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем  .
.
1) Не отказал ни один прибор.

2) Отказал один из приборов.
 0,302.
0,302.
3) Отказали два прибора.

4) Отказали три прибора.
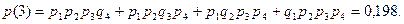
5) Отказали все приборы.

Получаем закон распределения:
| x | |||||
| x2 | |||||
| p | 0,084 | 0,302 | 0,38 | 0,198 | 0,036 |
Математическое ожидание:

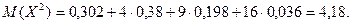
Дисперсия:

Вопросы для самоконтроля:
- Числовые характеристики случайных величин.
- Формула математического ожидания.
- Формула дисперсии.
- Формула среднего квадратического отклонения.
- Свойства М(Х).
- Свойства Д(Х).
Рекомендуемая литература
Основная:
- Общий курс высшей математики для экономистов [Текст]: Учебник /Под ред. В. И. Ермакова.- М.: Инфра-М, 2008.- 656 с.- Гриф МО
- Тырсин, А. Н. Математика.Теория вероятностей и математическая статистика [Текст] : учебное пособие/ А. Н. Тырсин.- Челябинск : Челяб. гос. ун-т, 2007.- 235 c.
Дополнительная:
- Ухоботов, В. И. Математика [Текст]: учебное пособие/ В. И. Ухоботов.- Челябинск : Челяб. гос. ун-т, 2006.- 251 c.
2. Сборник задач по высшей математике для экономистов [Текст]: Учебное пособие.- 2-е изд., испр.- М.: Инфра-М, 2008.- 574 с.- Гриф УМО
Дата добавления: 2014-12-03; просмотров: 348; Мы поможем в написании вашей работы!; Нарушение авторских прав |