Распределение Пуассона

(Симеон Дени Пуассон (1781 – 1840) – французский математик)

Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р. Если число испытаний п достаточно велико, а вероятность появления события А в каждом испытании мало (p£0,1), то для нахождения вероятности появления события А k раз находится следующим образом.

Сделаем важное допущение – произведение пр сохраняет постоянное значение:

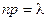
Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном п) остается неизменным.

По формуле Бернулли получаем:

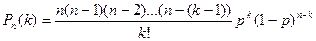
Найдем предел этой вероятности при п®¥.

Получаем формулу распределения Пуассона:

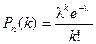
Если известны числа l и k, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона.

Тестовые вопросы для самоконтроля:

1. Схема Бернулли это:

а) схема повторных испытаний

б) единичное событие в) независимое событие

2. При больших nикискомую вероятность можно вычислить по формуле:

а) Бернулли б) Пуассона в) Лапласа

3. При больших nи маломpдля нахожденияискомой вероятности применяем формулу:

а) Бернулли б) Пуассона в) Лапласа

4. Определите наивероятнейшее число выпадений цифры при 5 бросаниях монеты:

а) m₀ =2 б) m₀ =3 в) m₀ ^/= 2, m₀^//=3

5. В университете 1095 студентов. Какова вероятность, что 1 января является днем рождения 5 студентов?

а) 0,5 б) 0,1008 в) 0,1095

6. К случайной величине Х прибавили постоянную а. Как изменится ее математическое ожидание?

а) увеличится в а раз; б) увеличится на а;

в) не увеличится.

7. К случайной величине Х прибавили постоянную а. Как изменится ее дисперсия?

а) не изменится; б) увеличится на а; в) уменьшится на а.

8. Случайную величину Х умножили на а. Как изменится ее математическое ожидание?

а) умножится на а ; б) умножится на а²; в) не изменится.

9. К случайной величине Х прибавили постоянную а.

Как изменится ее среднее квадратическое отклонение?

а) не изменится; б) прибавится а; в) умножится на .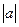

10. Какую из формул считаете верной?

а) М(СХ)=С² М(Х), б) Д(СХ)=С² Д(Х),

в) σ (СХ)=С²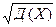

Рекомендуемая литература

Основная:

1. Общий курс высшей математики для экономистов [Текст]: Учебник /Под ред. В. И. Ермакова.- М.: Инфра-М, 2008.- 656 с.- Гриф МО
2. Тырсин, А. Н. Математика.Теория вероятностей и математическая статистика [Текст] : учебное пособие/ А. Н. Тырсин.- Челябинск : Челяб. гос. ун-т, 2007.- 235 c.

Дополнительная:

1. Сборник задач по высшей математике для экономистов [Текст]: Учебное пособие.- 2-е изд., испр.- М.: Инфра-М, 2008.- 574 с.- Гриф УМО