Лекция 4. Основные позиционные задачи.

Основными позиционными задачами называются задачи на определение взаимного расположения точки, прямой и плоскости.

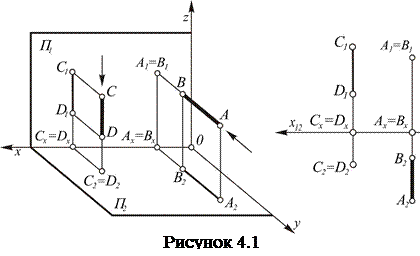Для определения видимости на чертеже применяется метод конкурирующих точек. Конкурирующими называются точки, расположенные на одной проецирующей прямой. На рисунке 4.1 (АВ) ^П₁, следовательно точки А и В – фронтально-конкурирующие. (СD) ^П₂, поэтому точки С и D – горизонтально-конкурирующие. Точка С находится выше точки D, поэтому точка С является видимой на горизонтальной проекции. Ордината точки А больше, чем точки В, поэтому точка А находится ближе к зрителю, следовательно, она является видимой на фронтальной проекции.

Прямые и точки, лежащие в плоскости. Прямая принадлежит плоскости, если две ее точки принадлежат данной плоскости. На рисунке 4.2 показана прямая l, принадлежащая плоскости a(bÇc), поскольку имеет с нею две общие точки – В и С.

Точка принадлежит плоскости, если она расположена на прямой, принадлежащей данной плоскости. Для того чтобы построить в плоскости a(bÇc) точку K (рисунок 4.2), необходимо провести в плоскости прямую l, принадлежащую плоскости a(bÇc), а затем задать на ней точку K, которая принадлежит прямой l и, следовательно, плоскости a(bÇc).

Главные линии плоскости. Среди множества прямых, которые могут быть проведены в плоскости, следует выделить главные линии плоскости:

1. Горизонтали – прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекций (рисунок 4.3а). Фронтальная проекция горизонтали горизонтальна.

3. Линии наибольшего ската(наклона) - прямые, принадлежащие данной плоскости и перпендикулярные горизонталям (или фронталям) плоскости. На рисунке 4.4 показана линия наибольшего ската MN плоскости a.

Следует отметить, что следы плоскости также являются главными линиями плоскости – горизонталью и фронталью, совмещенными с плоскостями проекций. Главные линии плоскости в качестве вспомогательных прямых облегчают решение ряда задач.

Взаимное положение двух плоскостей. Две плоскости в пространстве могут быть параллельными или пересекающимися. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым второй плоскости. Если параллельные плоскости задаются на эпюре следами, то одноименные следы этих плоскостей должны быть параллельны. На рисунке 4.5 плоскость a(aÇb) параллельна плоскости b(сÇd), поскольку с || а (с₁ || а₁, с₂ || а₂ ), d || b (d₁ || b₁, d₂ || b₂ ) .

Рассмотрим частный случай пересечения плоскостей, когда одна из них – проецирующая (рисунок 4.6). Если одна из пересекающихся плоскостей проецирующая, то одна из проекций линии пересечения совпадает с ее проецирующим следом.

Рассмотрим общий случай пересечения, когда обе плоскости – общего положения. На рисунке 4.7а приведены две плоскости a и b, заданные следами. Общими точками плоскостей являются точки М и N одноименных следов. Соединяя одноименные проекции этих точек прямой линией, получим проекции линии пересечения плоскостей.

Если точки пересечения одноименных следов находятся вне поля чертежа, а также в тех случаях когда плоскости заданы не следами, а другими геометрическими элементами, то для определения линии пересечения плоскостей следует использовать вспомогательные проецирующие плоскости или плоскости уровня. На рисунке 4.7б показаны две плоскости общего положения, заданные треугольником и двумя параллельными прямыми. Для определения двух общих точек линии пересечения плоскостей проводим две вспомогательные плоскости уровня g и d.

Прямая параллельна плоскости, если она параллельна прямой, принадлежащей этой плоскости.

Если прямая не принадлежит плоскости и не параллельна ей, то она пересекает данную плоскость. Задача на пересечение прямой линии с плоскостью является одной из основных задач начертательной геометрии. Если плоскость занимает проецирующее положение, то одна проекция точки пересечения определяется в пересечении проекции прямой с проецирующим следом плоскости, а другая строится с помощью линии связи (рисунок 4.8).

Если плоскость общего положения, точка пересечения прямой с плоскостью определяется с помощью вспомогательной секущей плоскости.

Для построения точки пересечения прямой линии l с плоскостью a(АВС) необходимо(рисунок 4.9):

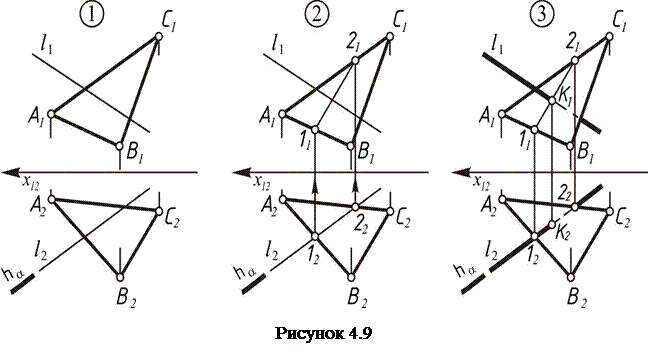1) провести через прямую l вспомогательную проецирующую плоскость b; 2) построить линию MN пересечения данной плоскости a и вспомогательной плоскости b; 3) определить искомую точку К пересечения данной прямой l с линией пересечения плоскостей MN (в случае если l || MN, то прямая l параллельна плоскости a, если l Î MN, то прямая l принадлежит плоскости a).

Основная литература: 1 осн.[43-62 ], 2 осн. [40-66 ]

Дополнительная литература: 1 доп.[20-29].

Контрольные вопросы:

1. Когда прямая принадлежит плоскости?

2. Когда точка принадлежит плоскости?

3. Перечислите и изобразите главные линии плоскости.

4. В каком случае прямая параллельна плоскости?

5. Как по чертежу установить параллельность двух плоскостей?

6. Перечислите этапы построения точки пересечения прямой с плоскостью общего положения.