Лекция 5. Многогранники.

Многогранной поверхностью называется поверхность, образованная частями(отсеками) пересекающихся плоскостей. Многогранником называется тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников. Отсеки плоскостей называются гранями, а линии их пересечения - ребрами. Точки пересечения ребер называются вершинами. Совокупность ребер и вершин многогранной поверхности называется сеткой.

Наиболее распространенные многогранники – призмы и пирамиды. Призму, ребра которой перпендикулярны к основанию, называют прямой. Если в основании прямой призмы – прямоугольник, призму называют параллелепипедом.

Многогранник, одна из граней которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину, называется пирамидой.

Среди большого числа разновидностей многогранников особую группу составляют правильные выпуклые многогранники.

Правильными многогранниками (Платоновыми) называются многогранники, у которых все грани – правильные и равные многоугольники, а углы при вершинах равны. Около каждого многогранника можно описать сферу и, наоборот, в каждый многогранник можно вписать сферу.

Существуют пять правильных многогранников:

1. Тетраэдр (четырехгранник) ограничен четырьмя равносторонними и равными треугольниками. Тетраэдр – правильная трехгранная пирамида.

2. Гексаэдр (шестигранник), или куб. Его поверхность состоит из шести равных квадратов..

3. Октаэдр (восьмигранник). Его поверхность состоит из восьми равных треугольников. Куб и октаэдр имеют одинаковое число ребер. В октаэдр можно вписать куб, а в куб – октаэдр, так чтобы вершины одного многогранника совпадали с центром граней другого. Такие многогранники называются взаимно соответствующими

4. Додекаэдр (двенадцатигранник) ограничен двенадцатью равносторонними и равными пятиугольниками. Около каждой вершины соединены три пятиугольника. Додекаэдру соответствует правильный двадцатигранник.

5. Икосаэдр (двадцатигранник). Его поверхность состоит из двадцати равносторонних и равных треугольников, соединенных по пяти около каждой вершины. В икосаэдр можно вписать додекаэдр. Икосаэдр и додекаэдр являются взаимно соответствующими многогранниками.

Тетраэдр взаимно соответствует самому себе.

У каждой пары взаимно соответствующих многогранников число граней одного многогранника соответствует числу вершин другого, а количество ребер у них одинаково.

Таблица 5.1

Наименование	Форма грани	Г	В	Р
Тетраэдр
Гексаэдр (куб)
Октаэдр
Додекаэдр
Икосаэдр

Свойства многогранников изучал Эйлер, ему принадлежит теорема, устанавливающая зависимость между числом граней (Г), вершин (В) и ребер (Р) выпуклых многогранников всех видов.

Теорема. У всякого выпуклого многогранника число граней плюс число вершин минус число ребер равно двум, т.е. Г + В – Р =2.

Видимость ребер многогранника. Для определения видимости применяется способ конкурирующих точек (рисунок 5.1). Внешний контур проекций многогранника всегда видимый. Видимость ребер внутри контура следует определять на каждой проекции отдельно, рассматривая взаиморасположение ребер.

На рисунке 5.1 даны проекции четырехгранника. На фронтальной проекции конкурирующими точками скрещивающихся ребер являются точки 1 и 2, а на горизонтальной проекции – точки 3 и 4. Анализ взаиморасположения конкурирующих точек позволяет установить, что на фронтальной проекции ребро АD будет видимым, а ребро ВС – невидимым. На горизонтальной проекции ребро BD будет видимым, а ребро АС – невидимым.

Пересечение многогранника плоскостью.Линией пересечения поверхности многогранника плоскостью является плоский многоугольник, вершины и стороны которого определяются пересечением заданной плоскости соответственно с ребрами и гранями данного геометрического тела. Таким образом, для построения сечения находят или точки пересечения ребер с заданной плоскостью или строят прямые, по которым плоскость пересекается с гранями многогранника. Первый способ называют способом ребер, второй – способом граней.

Построение сечений значительно упрощается, если секущая плоскость является проецирующей. В этом случае одна проекция сечения совпадет с проецирующим следом плоскости. На рисунке 5.2 фронтальная проекция А₁,В₁,С₁ сечения совпадает с фронтальным следом a₁ секущей плоскости. Проведя линии связи до горизонтальных проекций соответствующих ребер многогранника, получим горизонтальную проекцию сечения.

Пересечение прямой призмы плоскостью общего положения. Секущая плоскость задана двумя пересекающимися прямыми – горизонталью и фронталью. Так как боковые грани призмы – горизонтально проецирующие плоскости, горизонтальная проекция сечения известна, она совпадает с горизонтальной проекцией боковых граней и ребер призмы. Для построения фронтальной проекции сечения необходимо спроецировать точки А, В, С, принадлежащие секущей плоскости, на фронтальную проекцию. Через точки А₂ и В₂проведем горизонтальную проекцию (1₂2₂) прямой (1,2). На фронтальной проекции (1₁2₁) находим фронтальные проекции А₁, В₁. Через точку С проводим горизонтальную проекцию f´₂ фронтали f´, а затем строим ее фронтальную проекцию. В пересечении с соответствующим ребром призмы получим искомую проекцию точки С.

Пересечение пирамиды плоскостью общего положения. В отличие о предыдущей задачи, здесь необходимо построить обе проекции сечения. Горизонтальный след секущей плоскости не пересекает основание пирамиды, следовательно, пересекается ее боковая поверхность. Сечение должно иметь форму треугольника, вершинами которого будут точки пересечения ребер пирамиды с плоскостью. Точка пересечения D ребра SC с плоскостью a(fÇh) найдена с помощью фронтально проецирующей плоскостью b. Таким же образом можно определить и точку Е сечения. Но можно применить и другой прием. Продолжим ребро АС, которое является горизонтальным следом грани АСS пирамиды, до пересечения с горизонтальным следом секущей плоскости в точке 3. Точки D и 3 принадлежат линии пересечения ED данной грани и секущей плоскости. Построим точку F таким же способом, так как вспомогательная секущая плоскость, проведенная через ребро BS, будет параллельна профильной плоскости проекций и не даст решения. Точка 4 является точкой пересечения горизонтальных следов грани ABS и секущей плоскости. Соединив полученные точки прямыми и выделив на фронтальной проекции невидимый участок DE сечения, закончим построения.

Пересечение прямой линии с многогранником (рисунок 5.5). Эта задача решается в три этапа: 1) через данную прямую проводят секущую плоскость; 2) строят линию пересечения многогранника с секущей плоскостью; 3) определяют точки пересечения данной прямой с контуром сечения.

Линия пересечения двух многогранников представляет собой пространственную замкнутую линию. В частных случаях эта ломаная может распадаться на две замкнутые ломаные линии. Вершинами ломаной являются точки пересечения ребер одного многогранника с гранями другого. Стороны представляют собой отрезки прямых, по которым пересекаются грани многогранников. Построения упрощаются, если вершины и стороны ломаной определяются соответственно как точки и прямые пересечения граней общего положения одного многогранника с проецирующими ребрами и гранями другого. При построении линии пересечения поверхностей двух пирамид, призмы и пирамиды, двух призм в качестве вспомогательных плоскостей можно использовать плоскости общего положения:

1. две пирамиды – вспомогательные плоскости должны проходить через вершины пирамид;

2. пирамида и призма – вспомогательные плоскости, проходящие через вершину пирамиды параллельно боковым ребрам призмы;

3. две призмы – вспомогательные плоскости, параллельные боковым ребрам обеих призм.

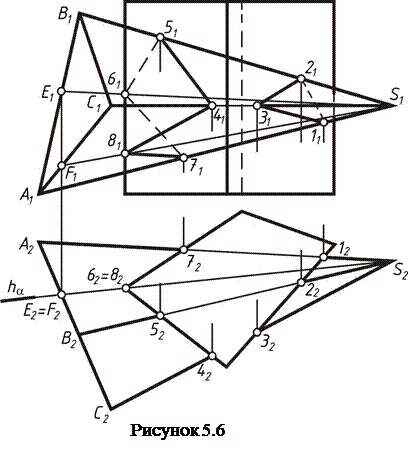Пересечение пирамиды с прямой призмой. Боковые ребра призмы проецируются в точки, а боковые грани являются горизонтально проецирующими отсеками плоскостей. Поэтому, одна проекция линии пересечения многогранников известна. Точки пересечении пирамиды с призмой легко определяется на горизонтальной проекции. С помощью линии связи строим фронтальные проекции этих точек. Из вертикальных ребер призмы лишь одно пересекает пирамиду. Точки пересечения этого ребра определяем с помощью вспомогательной горизонтально проецирующей плоскости, проходящей через данное ребро и вершину пирамиды. Соединяем построенные проекции точек, при этом следует руководствоваться горизонтальной проекцией.

Основная литература: 1 осн.[95-116 ], 2 осн. [111-146 ]

Дополнительная литература: 1 доп.[37-57].

Контрольные вопросы:

1. Дайте определение многогранника. Перечислите элементы многогранника.

2. Какие многогранники называются правильными?

3. Изложите сущность построения сечения многогранника плоскостью общего положения.

4. Изложите алгоритм построения точек пересечения прямой линии с многогранником.

5. Изложите сущность двух способов построения линии взаимного пересечения многогранников.