Перпендикулярность прямой и плоскости.

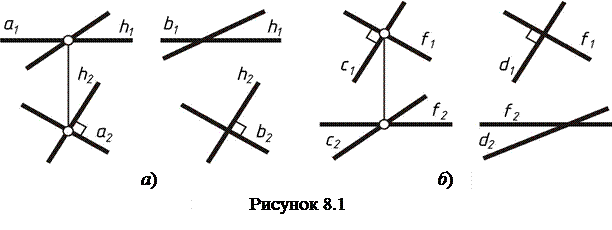
Теорема. Для того, чтобы прямая была перпендикулярна плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали, а фронтальная проекция - к фронтальной проекции фронтали этой плоскости.

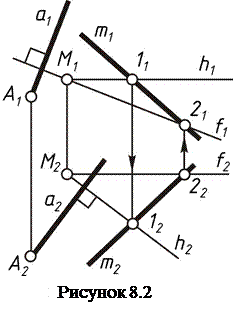
Пример 8.1. Построить проекции прямой а, проходящей через точку А и перпендикулярной плоскости a(М, m).

Сначала построим какую-нибудь горизонталь и фронталь плоскости a. Для простоты горизонталь h и фронталь f плоскости a проведены через ее точку М. Искомая фронтальная проекция а₁ прямой а проведена через точку А₁ перпендикулярно прямой f₁, а искомая горизонтальная проекция а₂ прямой а проведена через точку А₂ перпендикулярно h₂.

Признаки взаимной перпендикулярности плоскостей. Плоскость a перпендикулярна плоскости b, если она проходит через прямую а, перпендикулярную плоскости b, или она перпендикулярна прямой b, лежащей в плоскости b.

Через фиксированную точку М в пространстве можно провести сколько угодно плоскостей a¹, a², …, перпендикулярных заданной плоскости b. Все эти плоскости проходят через перпендикуляр а, опущенный из точки М на плоскость b. Совокупность плоскостей a¹, a², …, проходящих через прямую а, образует пучок плоскостей. Для фиксирования одной из этих плоскостей нужно иметь еще одно дополнительное условие.

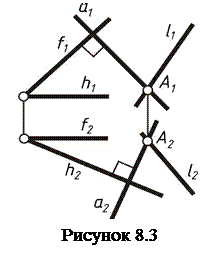
Пример8.2. Построить проекции плоскости b , проходящей через заданную прямую l(l₁,l₂) и перпендикулярную заданной плоскости a(hÇf) (рисунок 8.3).

Возьмем произвольную точку А на прямой l. Из точки А опустим перпендикуляр а на плоскость a, т.е. А₁Ì(а₁)^f₁, А₂Ì(а₂)^h₂. Прямые а и l, которые пересекаются в точке А, определяют некоторую плоскость b. Плоскость b проходит через прямую а и перпендикулярна плоскости a.

Построение взаимноперпендикулярных прямых общего положения. Две прямые перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость , перпендикулярную другой прямой.

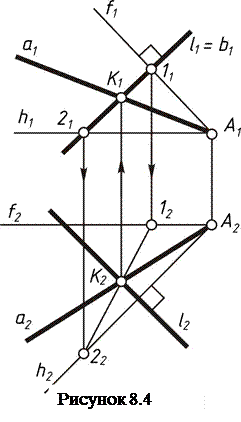
Пример 8.3. Через точку А провести прямую а, пересекающую заданную прямую l под прямым углом (рисунок 8.4). Через точку А проведем плоскость a перпендикулярно прямой l: А₁Ì(f₁)^l₁; А₂Ì(h₂)^l₂; А₁Ì(h₁)^A₁ A₂; А₂Ì(f₂)^ A₁ A₂; a(hÇf). Плоскость a определена горизонталью h и фронталью f. Любая прямая плоскости a перпендикулярна прямой l, но среди них существует лишь единственная прямая, пересекающая прямую l. Находим точку пересечения прямой l с плоскостью a. (К)=lÇ a. Прямая а, определяемая двумя точками А и К, проходит через точку А и перпендикулярна прямой l, так как аÌ a^l.

Определение длины отрезка прямой. Ортогональные проекции отрезка прямой общего положения всегда меньше длины самого отрезка (рисунок 8.5). Длину отрезка прямой АВ можно определить по двум его проекциям из прямоугольного треугольника А₂В₂А₀, в котором одним катетом является горизонтальная проекция А₂В₂ отрезка, а другим катетом – разность координат его концов Dz, взятая из другой проекции. Гипотенуза А₀В₂ прямоугольного треугольника есть длина отрезка. Угол a в этом треугольнике определяет угол наклона к плоскости П₂. Длину отрезка прямой можно определить аналогичным образом, построив прямоугольный треугольник на фронтальной проекции отрезка. Угол b в этом треугольнике определяет наклон прямой к плоскости П₁.

Способы преобразования чертежа.Построение новых проекций оригинала по данным его проекциям называется преобразованием чертежа. Различают два метода преобразования чертежа:

1. Преобразование чертежа изменением положения оригинала относительно основных плоскостей проекций П₁, П₂, П₃.

2. Преобразование чертежа введением дополнительной плоскости проекций.

Основные задачи преобразования проекций.

Метод преобразования чертежа изменением положения оригинала относительно основных плоскостей проекций состоит в том, что оригинал перемещается относительно П₁, П₂, П₃ и ставится в такое положение, которое удобно для решения конкретной задачи. В зависимости от вида движения, которому подвергается оригинал, различают:

а) способ плоскопараллельного перемещения;

б) способ вращения вокруг проецирующих осей;

в) способ вращения вокруг прямой уровня.

Способ плоскопараллельного перемещения.

Плоскопараллельным перемещением предмета называется такое его движение, при котором все точки предмета перемещаются в плоскостях, параллельных между собой. В плоскопараллельном перемещении относительно плоскости П₁ все точки движущегося предмета перемещаются во фронтальных плоскостях уровня, в плоскопараллельном перемещении относительно плоскости П₂ – в горизонтальных плоскостях уровня. Для того, чтобы построить проекции в конечном ее положении нужно знать инварианты преобразования чертежа. Инвариантами преобразования называются такие правила, позволяющие по проекциям данного положения предмета найти проекции его конечного положения. Инварианты плоскопараллельного перемещения относительно плоскости П₁:

1. Фронтальная проекция перемещающейся фигуры движется по плоскости П₁, оставаясь равной самой себе;

2. Горизонтальные проекции точек фигуры перемещаются по фронтальным прямым, перпендикулярным к вертикальным линиям связи.

Основные задачи, решаемые преобразованием чертежа.

Все задачи, решаемые преобразованием чертежа, сводятся к четырем основным задачам. Покажем решения этих четырех задач способом плоскопараллельного перемещения.

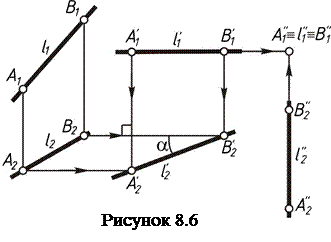
Задача 1. Сделать прямую общего положения прямой уровня. Если мы хотим прямую l сделать горизонталью, то ее следует подвергать 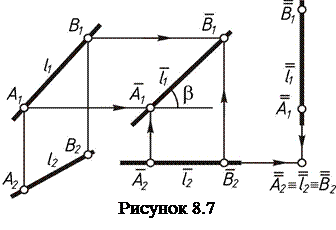плоскопараллельному перемещению относительно П₁ (рисунок 8.6). Отметим две произвольные точки А и В прямой l. Вычерчиваем горизонтальную прямую и, отложив на ней отрезок А´₁В´₁= А₁В₁, примем ее за новую фронтальную проекцию l´₁ горизонтальной прямой l´. При этом горизонтальные проекции точек А и В остаются на горизонтальных прямых, проходящих через точки А₂ и В₂. По новым фронтальным проекциям А´₁ и В´₁ определяем их новые горизонтальные проекции А´₂ и В´₂. Если мы хотим прямую l сделать фронталью, то ее следует подвергать плоскопараллельному перемещению относительно П₂.(рисунок 8.7).

В результате решения этой задачи мы нашли натуральную величину отрез 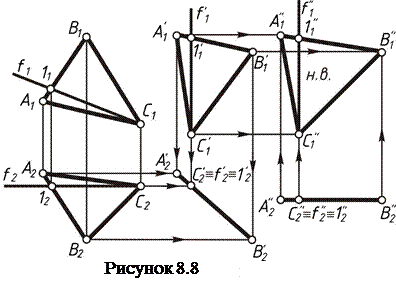ка АВ прямой l 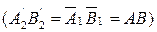и углы ее наклона a и b к основным плоскостям проекций П₁ и П₂.

Задача 2. Сделать прямую уровня проецирующей прямой. Если дана горизонтальная прямая l´(l₁´, l₂´) , то проще всего сделать ее фронтально проецирующей прямой l´´(рисунок 8.6). Для этого вычерчиваем вертикальную прямую и, отложив на ней отрезок А₂″В₂″= А´₂В´₂, примем ее за новую горизонтальную проекцию l₂″ фронтально проецирующей прямой l″. Новая фронтальная проекция l₁″ вырождается в точку А₁″≡В₁″≡l₁″.

Из фронтальной прямой 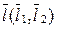проще всего сделать горизонтально проецирующую прямую 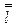(рисунок 8.7). Для этого сначала вычерчиваем новую фронтальную проекцию в виде вертикальной прямой, а затем – новую вырожденную в точку горизонтальную проекцию.

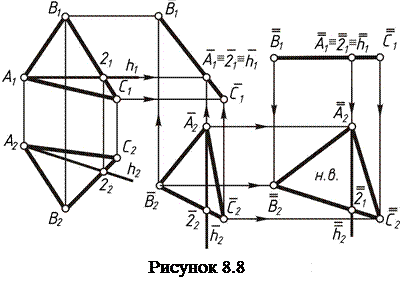
Задача 3. Привести плоскость общего положения в положение проецирующей плоскости. Если мы хотим сделать плоскость a(АВС) горизонтально проецирующей плоскостью, то ее следует подвергать плоскопараллельному перемещению относительно П₁ (рисунок 8.8). Проводим произвольную фронталь f плоскости a и сделаем ее горизонтально проецирующей прямой f ´. Новая фронтальная проекция А´₁В´₁ С´₁ треугольника АВС строится так, чтобы f ₁´ занимала вертикальное положение и 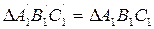. Находим новые горизонтальные проекции А₂´, В₂´, С₂´, которые располагаются на одной прямой. В новом положении a ´ плоскость a стала горизонтально проецирующей.

Если мы хотим сделать плоскость a фронтально проецирующей плоскостью, то следует ее подвергать плоскопараллельному перемещению относительно плоскости П₂ (рисунок 8.9).

Задача 4. Привести проецирующую плоскость в положение плоскости уровня. Если дана горизонтально проецирующая плоскость a ´, то следует ее сделать фронтальной плоскостью плоскопараллельным перемещением относительно плоскости П₂ (рисунок 8.8). Для этого вычерчиваем горизонтальную прямую и на ней отмечаем точки А₂″, В₂″, С₂″ так, чтобы А₂″В₂″= А₂´В₂´ и В₂″С₂″= В₂´С₂´.Проводим через точки А´₁,В´₁, С´₁ горизонтальные прямые, а через точки А₂″, В₂″, С₂″ - вертикальные прямые. В пересечении прямых проведенных через проекции одноименных точек, получаем новые фронтальные проекции А₁″, В₁″, С₁″. Если дана фронтально проецирующая плоскость 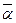, то следует ее сделать горизонтальной плоскостью плоскопараллельным перемещением относительно плоскости П₁ (рисунок 8.9). В результате решения этой задачи мы получаем на чертеже натуральную величину треугольника АВС: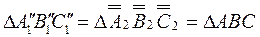

Основная литература: 1 осн.[27, 60-62 ], 2 осн. [40-56 ]

Дополнительная литература: 1 доп.[20-29].

Контрольные вопросы:

1. Какие задачи называются метрическими?

2. Сформулируйте теорему о прямоугольной проекции прямого угла.

3. Сформулируйте условие перпендикулярности прямой и плоскости.

4. Когда прямой угол проецируется без искажения на горизонтальную плоскость проекций?

5. Сформулируйте условие перпендикулярности двух плоскостей.

6. В чем сущность преобразования плоскопараллельным перемещением?

7. Перечислите основные четыре задачи, решаемые преобразованием.