Лекция 10. Кривые линии и поверхности.

Кривая (линия) – это однопараметрическое множество точек. Кривые линия в начертательной геометрии рассматривается как траектория, непрерывно движущейся в пространстве точки, а также как линия пересечения поверхностей.

Типы линий –плоские, все точки которой принадлежат одной плоскости – (окружность, эллипс, парабола, гипербола), пространственные –все точки не принадлежат одной плоскости - винтовые (цилиндрические, конические и т.д.). Кривая может быть описана аналитически, т.е. уравнением (алгебраическим или трансцендентным), например, эллипс, парабола, гипербола и др. Если образование кривой не имеет строгой закономерности, то она задается графически, например горизонтали на плане местности.

Степень уравнения, которое выражает алгебраическую кривую, определяет порядок кривой. Геометрически порядок плоской кривой определяется числом точек ее пересечения прямой линией (как действительных, так и мнимых точек). Порядок пространственной кривой определяется числом точек пересечения кривой с плоскостью.

Свойства проекций кривой: 1) в общем случае проекции кривой линии является также кривыми линиями; 2) если точка принадлежит кривой линии, то ее проекции принадлежат одноименным проекциям этой кривой; 3) касательная к кривой линии проецируется в касательную к проекции этой кривой, если направление не параллельно касательной. Точка кривой называется обыкновенной, если в этой точке можно построить единственную касательную к кривой. Точка называется особой, если в ней не определено положение касательной. К ним относятся (рисунок 10.1): а) угловая точка, в которой кривая имеет две касательные и направление ее изменяется «скачком»; б) узловая точка, в которой кривая пересекает себя; в) точка перегиба, в которой изменяется направление движения касательной; г) точки возврата первого рода; д) точка возврата второго рода.

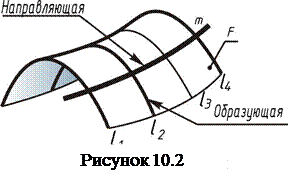Образование и задание поверхности. В начертательной геометрии поверхность рассматривается как непрерывное множество последовательных положений линии, перемещающейся в пространстве по определенному закону. Такой способ образования поверхностей называется кинематическим. Линию l, которая при своем движении образует поверхность, называют образующей (рисунок 10.2). Образующая может перемещаться по какой-либо другой неподвижной линии m, называемой направляющей. Совокупность геометрических элементов и условий, необходимых и достаточных для однозначного задания поверхности называют определителем. Определитель поверхности содержит две части – геометрическую и алгоритмическую.

Поверхность считается заданной, если относительно любой точки пространства можно решить вопрос о ее принадлежности данной поверхности.

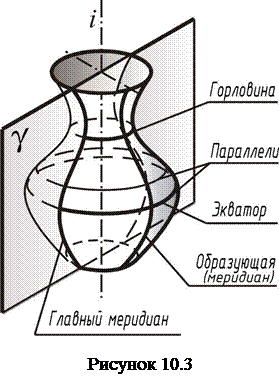
Поверхностью вращения называется поверхность, образованная вращением линии – образующей вокруг неподвижной прямой – оси вращения.

На проекционном чертеже ось вращения располагают перпендикулярно плоскости проекций. Окружности, по которым перемещаются все точки образующей называются параллелями. Наибольшую параллель называют экватором, наименьшую – горловиной. Если ось вращения вертикальна, то все параллели проецируются на горизонтальной проекции без искажения. Плоскости, проходящие через ось вращения, пересекают поверхность по линиям, называемым меридианами. Меридиан, расположенный в плоскости, параллельной плоскости проек 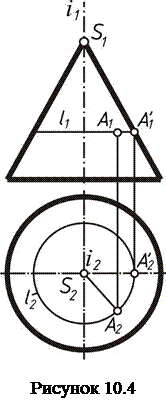ций, называется главным и проецируется на эту плоскость проекций очерком поверхности.

На рисунке 10.4 показано как определять недостающую проекцию точки А, если задана ее только одна проекция на поверхности вращения.

При вращении прямой l вокруг оси i образуется линейчатая поверхность вращения второго порядка:

если l Ç i - коническая поверхность вращения;

если l ÷÷ i - цилиндрическая поверхность вращения;

если l i - однополостный гиперболоид вращения.

Вид поверхности вращения зависит от формы образующей и ее положения относительно оси вращения. При вращении кривой n-го порядка, имеющей плоскость симметрии, вокруг оси, лежащей в этой плоскости, образуется поверхность вращения n-го порядка.

1. Сфера. Образуется вращением окружности вокруг диаметра.

2. Эллипсоид вращения. Меридианом является эллипс. Если эллипс вращается вокруг большой оси, эллипсоид называется вытянутым, если вращение происходит вокруг малой оси, эллипсоид называют сжатым.

3. Параболоид вращения. Меридианом является парабола.

4. Гиперболоид вращения. Меридианом поверхности является гипербола. Если ось вращения совпадает с действительной осью гиперболы, образуется двуполостный гиперболоид, если осью вращения является мнимая ось, то – однополостный.

5. При вращении алгебраической кривой n-го порядка вокруг произвольной прямой образуется поверхность вращения порядка 2n. Например, тор. Поверхность тора образуется вращением окружности вокруг оси, не проходящей через ее центр, но расположенной в плоскости окружности.

Поверхность, образованная движением прямой линии по заданному закону, называется линейчатой. Развертываемые линейчатые поверхности – конические и цилиндрические, торсовые. Линейчатая поверхность, образованная множеством касательных пространственной кривой, называется торсовой или поверхностью с ребром возврата.

Неразвертываемые – поверхности с плоскостью параллелизма (поверхности Каталана): цилиндроид, коноид, косая плоскость (гиперболический параболоид) (рисунок 10.5).

Поверхность, образованная винтовым движением некоторой линии, называется винтовой поверхностью. Если при своем движении образующая пересекает ось винтового движения, то поверхность называется закрытой, в противном случае – открытой. Если образующей является прямая, то поверхность назвается геликоидом. Геликоид называется прямым, если образующая перпендикулярна оси винтового движения, в противном случае – наклонным. На рисунке 10.6 показан закрытый прямой геликоид. Если образующие открытого геликоида являются касательными некоторой цилиндрической винтовой линии, то геликоид называется винтовым торсом или эвольвентным, так как его нормальное (перпендикулярное оси) сечение представляет эвольвенту окружности.

Поверхность, образованная параллельным перемещением образующей l по направляющей m, называется поверхностью параллельного переноса.

Основная литература: 1 осн.[117-162 ], 2 осн. [67-93 ]

Дополнительная литература: 1 доп.[57-84].

Контрольные вопросы:

1. Какие кривые линии называются алгебраическими и какие - трансцендентными?

2. Какие точки кривой относят к особым?

3. Что называется определителем поверхности?

4. Укажите основные свойства поверхностей вращения?

5. Какие винтовые поверхности называют геликоидами?

6. Как построить точку и линию, принадлежащие поверхности?

7. Назовите поверхности вращения с прямолинейной образующей.