Лекция 12. Взаимное пересечение поверхностей.

Для построения линии пересечения чаще всего используется способ вспомогательных поверхностей. Алгоритм решения задачи способом вспомогательных поверхностей может быть описан в общем виде следующим образом. Линией пересечения может быть прямая, плоская и пространственная кривая или любое сочетание из этих линий.

Построим одну из точек линии пересечения поверхностей F и W. Для этого проведем поверхность S, которая пересекается F по кривой а, а с W - по кривой b. Точка А пересечения кривых а и b принадлежит обеим заданным поверхностям, следовательно, и линии их пересечения с. Аналогично, может быть найдено любое число точек линии пересечения.

Чтобы построить линию пересечения двух поверхностей, следует рассечь их рядом вспомогательных поверхностей, построив линии пересечения поверхностей данных и вспомогательных, нужно отметить общие для них точки, эти точки должны быть последовательно соединены между собой.

Точки линии пересечения двух поверхностей делятся на опорные и промежуточные. К опорным точкам относятся:

1. самая близкая и самая удаленная точка линии пересечения относительно той или иной плоскости проекций;

2. точки видимости, имеющие проекции на линии очертания;

3. точки наибольшей ширины линии пересечения и т.д.

Построение линии пересечения поверхностей следует начинать с определения ее опорных точек.

В качестве вспомогательных поверхностей чаще всего следует брать плоскости, либо сферы. Поэтому, из общего способа выделяют два, которые называются способом вспомогательных плоскостей и способом сфер.

Способ вспомогательных плоскостей. В качестве вспомогательных плоскостей могут быть приняты:

1. плоскости уровня;

2. проецирующие плоскости;

3. плоскости общего положения.

Пример. Построить пересечение трехгранной призмы с конусом вращения (рисунок 12.2). Три боковые грани призмы являются фронтально проецирующими плоскостями. Линия пересечения данных поверхностей представляет собой ломаную линию, состоящую из трех плоских кривых. Грани призмы пересекают поверхность конуса по окружности, неполному эллипсу и неполной параболе.

Частные случаи пересечения поверхностей второго порядка. Способ сфер.

При пересечении поверхностей второго порядка линией пересечения в общем случае является пространственная кривая четвертого порядка. Эта кривая пересекается плоскостью в четырех точках (действительных и мнимых). Порядок линии пересечения равен произведению порядков пересекающихся поверхностей. Кривая четвертого порядка может распадаться на две плоские кривые второго порядка.

Теорема: Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются и по второй кривой.

Справедливость этого положения вытекает из того, что сумма порядков кривых, на которых распалась линия пересечения поверхностей должна равняться четырем. Следовательно, должна существовать другая плоская кривая второго порядка, по которой пересекаются данные поверхности.

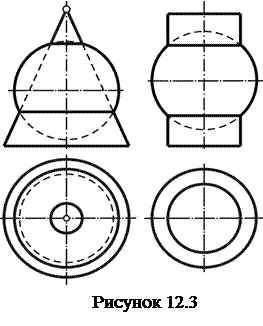
1. Оси двух пересекающихся поверхностей вращения совпадают.(рисунок 12.3)

Две соосные поверхности вращения пересекаются по параллелям, при этом, если оси поверхностей параллельны плоскости проекций, то параллели проецируются на эту плоскость прямыми линиями, перпендикулярными проекции оси.

2. Оси поверхностей вращения пересекаются и параллельны плоскости проекций.(рисунок 12.4). В этом случае нецелесообразно использовать вспомогательные секущие плоскости. Они не могут дать вспомогательные линии сечения, которые проецировались бы графически про стыми линиями. Поэтому для построения линии пересечения поверхностей вращения с пересекающимися осями и общей плоскостью симметрии, параллельной плоскости проекций следует применять способ вспомогательных концентрических сфер. Если оси поверхностей вращения второго порядка пересекаются и параллельны плоскости проекций, то линия их пересечения проецируется на эту плоскость в виде плоской кривой второго порядка.

3. Поверхности в точках касания имеют общие касательные плоскости (рисунок 12.5).

Теорема о двойном соприкосновении. Если две поверхности 2-го порядка имеют две точки соприкосновения и общие касательные плоскости в этих точках, то линия их пересечения распадается на две плоские кривые второго порядка.

4. Две пересекающиеся поверхности касаются третьей поверхности второго порядка (рисунок 12.6).

Теорема Г.Монжа. Если две поверхности 2-го порядка описаны вокруг третьей поверхности 2-го порядка или вписаны в нее, то они пересекаются по двум плоским кривым 2-го порядка.

Теорема Монжа – частный случай теоремы о двойном соприкосновении.

Основная литература: 1 осн.[191-200], 2 осн. [131-145]

Дополнительная литература: 1 доп.[103-116].

Контрольные вопросы:

1. Назовите основные способы построения линий пересечения поверхностей.

2. Изложите общие принципы выбора вспомогательных секущих плоскостей и сфер при построении линии пересечения поверхностей.

3. В каком случае поверхности вращения пересекаются по окружностям?

4. Какое пересечение поверхностей называют полным и неполным?

5. Какие точки линии пересечения поверхностей называют опорными (характерными)?