
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 13. Развертки многогранных и кривых поверхностей.
Разверткой многогранной поверхности называется плоская фигура, которая получена совмещением всех ее граней с одной плоскостью.
 Пример. Построить развертку поверхности пирамиды SABCD (рисунок 13.1).
Пример. Построить развертку поверхности пирамиды SABCD (рисунок 13.1).
|
 . Вторые катеты этих треугольников равны длинам горизонтальных проекций этих ребер. Для удобства построение натуральных величин боковых ребер вынесено на свободное поле чертежа. Совокупность треугольников
. Вторые катеты этих треугольников равны длинам горизонтальных проекций этих ребер. Для удобства построение натуральных величин боковых ребер вынесено на свободное поле чертежа. Совокупность треугольников 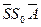 ,
, 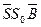 ,
,  ,
,  с общим катетом
с общим катетом  называется диаграммой натуральных величин.
называется диаграммой натуральных величин.
Построение развертки поверхности пирамиды ясно из приведенного чертежа, на котором конгруэнтные отрезки обозначены одинаковыми значками. К развертке боковой поверхности пирамиды пристраиваем ее основание.
Построение развертки поверхности призмы выполняется тремя способами:
1) способом треугольников (триангуляции),
2) способом нормальных сечений,
3) способом раскатки.
Способ треугольников является наиболее универсальным. Он пригоден для построения точных разверток любых многогранных поверхностей, а также для построения приближенных и условных разверток линейчатых поверхностей.
 Способ нормальных сечений применяется для построения разверток призматических поверхностей, если их боковые ребра являются прямыми уровня.
Способ нормальных сечений применяется для построения разверток призматических поверхностей, если их боковые ребра являются прямыми уровня.
Развертка поверхности призмы способом нормальных сечений выполняется в такой последовательности (рисунок 13.2):
1) призма пересекается плоскостью a, перпендикулярной ее боковым ребрам;
2) определяются натуральные величины сторон ломаной линии, по которой плоскость a пересекает поверхность призмы;
3) эта ломаная развертывается в отрезок прямой;
4) на перпендикулярах, проведенных к этой прямой в точках, соответственных вершинам ломаной, откладываются натуральные величины соответствующих отрезков ребер;
5) концы ребер последовательно соединяются отрезками прямых;
 6) к построенной развертке боковой поверхности призмы пристраиваются многоугольники, равные натуральным величинам оснований призмы.
6) к построенной развертке боковой поверхности призмы пристраиваются многоугольники, равные натуральным величинам оснований призмы.
Способ раскатки – частный случай способа нормальных сечений. Он применяется для построения разверток призматических поверхностей, если их боковые ребра и плоскости оснований являются соответственно прямыми и плоскостями уровня.
Сущность способа раскатки состоит в том, что грани призмы последовательными вращениями вокруг ее боковых ребер совмещаются с какой-либо плоскостью. Получающаяся при этом фигура является разверткой боковой поверхности призмы.
Построение приближенных разверток развертывающихся поверхностей (конических, цилиндрических и торсовых) сводится к построению точных разверток многогранных поверхностей, вписанных в данные поверхности или описанных около них. Построение приближенных разверток выполняется в такой последовательности:
1) данную развертывающуюся поверхность заменяют (аппроксимируют) многогранной поверхностью;
2) строят точную развертку многогранной поверхности;
3) точную развертку аппроксимирующей многогранной поверхности принимают за приближенную развертку данной развертывающейся поверхности.
Основная литература: 1 осн.[201-207], 2 осн. [105-110]
Дополнительная литература: 1 доп.[117-123].
Контрольные вопросы:
1. Что называют разверткой поверхностей?
2. Какие поверхности называются развертывающимися и какие - неразвертывающимися?
3. Укажите основные свойства разверток?
4. Укажите последовательность графических построений разверток поверхностей конуса и цилиндра?
5. Что называют аппроксимацией поверхности?
6. Какие способы разверток многогранников вы знаете?
Дата добавления: 2014-12-03; просмотров: 517; Мы поможем в написании вашей работы!; Нарушение авторских прав |