Зоряні величини

В астрономії освітленість, яку створюють зорі вимірюють в спектральній логарифмічній шкалі – зоряних величин. За інтервал в 1 зоряну величину прийнято інтервал освітленості в 2,512 раз. Це число вибрано для зручності так, щоб його десятковий логарифм дорівнював 0,4.

(lg 2,512 = 0,4),

а інтервал 5^m відповідав би відношенню 100 раз.

Освітленості від об’єктів –3^m, -2^m, -1^m, 0^m, 1^m, 2^m, 3^m,… утворюють спадну прогресію з знаменником 2,512.

Зоряною величиною називається взятий із знаком мінус логарифм при основі 2,512 від освітленості, яку створює даний об’єкт на площадці, перпендикулярній до променя.

Із означення випливає:

і

або в десяткових логарифмах:

=>

Зоря О^m утворює на межі земної атмосфери освітленість 2,78 * 10^-6 люкс

Абсолютна зоряна величина і світимість зір

Зоряна величина, яку б мала зоря, якби вона знаходилася на відстані 10nс називається абсолютною.

де Е і Е₀ – освітленості від зорі на віддалі r і 10 nс, тоді

Якщо абсолютна зоряна величина відома з інших вимірювань, то можна знайти віддаль до зір

lg r = 1 + 0,2 (m – M).

Величина (m – M) називається модулем віддалі.

Знайдемо абсолютну зоряну величину Сонця

= - 26,8 ^m = 1 a.o = 1 / 206265 ^nc

= - 26,8^m + 5^m + 26,6^m = 4,8^m

При визначенні зоряних величин безпосередньо із спостережень реєструється тільки та частина випромінювання, яка пройшла через атмосферу, дану оптичну систему і зареєстрована світлочутливим приладом. Для знаходження сумарного випромінювання слід ввести поправку на випромінювання, яке не дійшло до приладу. Зоряна величина, визначена з урахуванням випромінювання в усіх ділянках спектра називається болометричною.

Різницю між болометричною зоряною величиною і візуальною або фотографічною називають болометричною поправкою.

Δm_воl = m_воl – m_v = M_воl - M_v

Болометричні поправки обчислюють теоретично. Останнім часом для цього застосовують позаатмосферних вимірювань зір в ультрафіолетовій області спектра.

Болометрична поправка має мінімальне значення для тих зір, які у видимій області спектра випромінюють найбільшу частину своєї енергії і залежить від ефективності три зорі.

Таблиця - Болометричні поправки

Болометричні поправки дають можливість визначити болометричні світимості тих зір, для яких відомі абсолютні візуальні зоряні величини.

Нехай M_v – абсолютна візуальна зоряна величина деякої зорі.

Δm_вос – її болометрична поправка.

Тоді

Для Сонця :

Δm_воl = -0,1^m

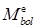= 4,8^m – 0,1^m = 4,7^m

Потік енергії, яку випромінює зоря в усіх напрямках називається світимістю (L).

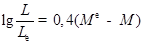
де L – світимість зорі, М – абсолютна зоряна величина зорі.

Якщо світимість Сонця прийняти за одиницю L_Θ = 1 , то

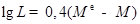
Залежно від методу визначення зоряних величин, які входять до даної формули одержимо візуальну, болометричну чи фотографічну світимість. Для болометричних світимостей одержимо

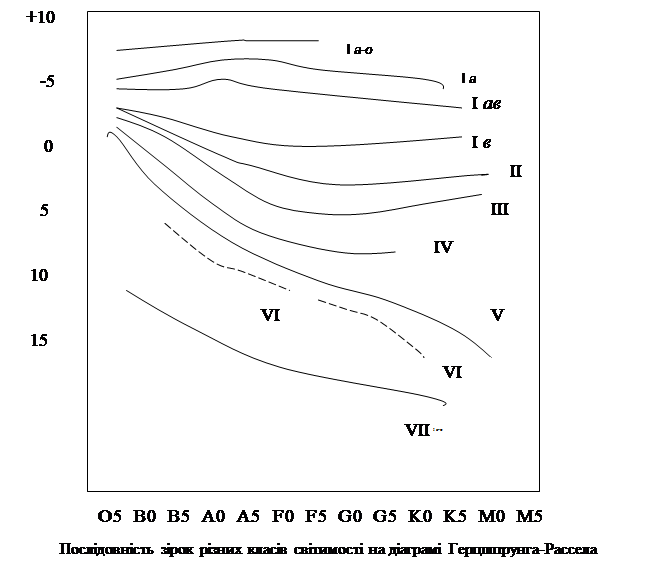
Діаграма спектр-світність

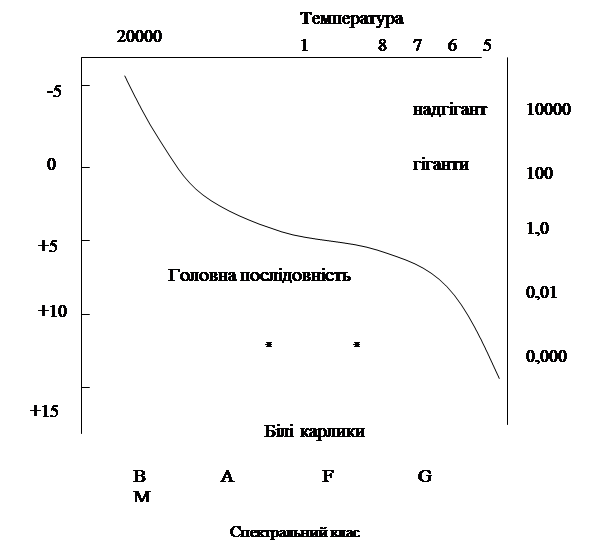На початку ХХ століття датський астроном Герцшпрунг і американський астрофізик Рессел виявили існування залежності між видом спектру (температурою) і світимістю зорі. Ця залежність зображується графіком по одній осі відкладаються спектральний клас, а по другій абсолютну зоряну величину. Цей графік називається діаграмою спектр-світимість, або діаграмою Герцшпрунга-Рессела.

Замість абсолютної зоряної величини можна відкладати світимість (в логарифмічній шкалі), а замість спектральних класів – показник кольору або ефективну температуру. Положення кожної зорі в тій чи іншій точці діаграми визначається її фізичною природою і стадією еволюції. Тому на діаграмі Герцшпрунга-Рессела ніби зображенався історіясистеми зір. В цьому і полягає її знання. Діаграма дає можливість виділити різні групи зір об’єднані спільними фізичними властивостями і встановити залежність між окремими фізичними характеристиками.

Верхня частина діаграми – зорі великої світимості, які при даному значенні температури відзначаються великими розмірами.

В нижній частині діаграми розташовані гарячі зорі більш ранніх класів.

В правій частині – більш холодні зорі, які відповідають пізнім спектральним класам.

У верхній частині діаграми знаходяться зорі, які мають найбільшу світимість (гіганти і надгіганти).

Зорі, які лежать в нижній частині діаграми мають низьку світимість і називаються карликами.

Найбагатшу зоряну діагональ, яка іде зліва вниз направо називають головною послідовністю. Вздовж неї розташовані зорі починаючи від найгарячіших до найхолодніших.

Зорі на діаграмі Герцшпрунга-Рессела розподілені не рівномірно, що відповідає існуванню певної залежності між світимістю і температурами всіх зір.

При уважному вивченні діаграми дає можливість виділити на ній ряд інших послідовностей (більш дисперсних ніж головна). Ці послідовності говорять про те, що у деяких окремих груп зір існує індивідуальна залежність від температури. Такі послідовності називаються класами світимості і позначають римськими цифрами від І до VII, проставленими після найменування класу.

Сонце відноситься до головної послідовності і попадає в V клас світимості.

Повна класифікація зір залежить від двох параметрів: перший характеризує спектр (температуру), другий – світимість.

Приналежність зір до класів:

Клас світимості І – надгіганти, ці зорі займають на діаграмі спектр-світимість верхню частину і діляться на декілька послідовностей.

ІІ – яскраві гіганти

ІІІ – гіганти

ІV - субгіганти

Зорі класу ІІ, ІІІ та ІV розташовані на діаграмі між областю надгігантів та головною послідовністю.

V – зорі головної послідовності.

VІ – яскраві субкарлики. Вони утворюють послідовність, яка проходить нижче головної приблизно на одну зоряну величину починаючи з класу АО.

VІІ – білі карлики.

Належність зір до даного класу світимості на основі спеціальних додаткових ознак спектральної класифікації