КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Физический смысл универсальной газовой постоянной.
Универсальная газовая постоянная имеет размерность работы, отнесенной к 1 молю и температуре 1°К.
Выясним физический смысл постоянной “R”.
Пусть в цилиндре под поршнем находится 1 моль газа объема V. Газ под поршнем оказывает давление равное внешнему постоянному давлению, т.е. p = const. Пусть газ в цилиндре нагревается на 1°К. Расширяясь, он поднимает поршень на высоту “h”, совершив при том работу 
, но давление на поршень 
, поэтому 
, здесь 
– приращение объема, т.е. 
, поэтому работа расширения будет равна
| (*) |
С другой стороны до нагревания уравнение состояния
| (1) |
после нагревания
| (2) |
Вычитая из (2) – (1), получим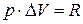 
. Сопоставляя со (*), имеем 
.
| Т.е. | универсальная газовая постоянная численно равна работе при изобарическом расширении 1 моля газа вследствие его нагревания на 1°К. | ЗАПОМНИТЬ |
ЗАМЕЧАНИЕ: Уравнение Клапейрона – Менделеева справедливо и для смеси газов. Пусть имеем смесь газов:
| Массы газов – | m1, m2, m3, …, mn |
| молярные массы газов – | m1, m2, m3, …, mn |
Введем величины: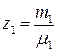 
; 
и т.д. Причем 
.
Уравнение Менделеева - Клапейрона для смеси газов запишется в виде:
.
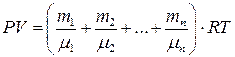Для того, чтобы упростить это выражение для смеси газов вводят понятие эффективного молекулярного веса смеси газов.
ОПРЕДЕЛЕНИЕ: Эффективным молекулярным весом называется вес такого газа, который при одинаковых параметрах со смесью газов имеет ту же массу, что и смесь газов.
; 
;
.
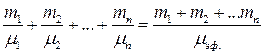Дата добавления: 2014-12-03; просмотров: 238; Мы поможем в написании вашей работы!; Нарушение авторских прав |