Этапы построения математической модели

Общей методологией исследования (моделирования) сложных систем является системный подход и сложившийся на его базе системный анализ. Действительно, объект системного анализа – абстрактная система – фактически является моделью, предметом системного анализа является процесс моделирования.

Методологической базой моделирования являются следующие системные принципы:

- всеобщая полнота описания системы принципиально невозможна;

- любое описание является упрощенным образом реальности, однако, даже самые сильные упрощения могут принести плодотворные результаты, если они отвечают цели исследования;

- корректность и продуктивность описания системы определяется степенью достижения цели исследования – получением частичного конкретного знания; допустимы различные (в том числе и несопоставимые) субъективные модели одной и той же объективной системы;

- личность исследователя включается в модель системы и, таким образом, в процессе исследования возникает новая система, включающая в себя наряду с изучаемой системой также ее исследователя с его научным аппаратом и субъективными качествами[5].

В соответствии с системным подходом можно построить «базовую» метамодель любой системы в виде открытого кортежа ее «базовых» признаков и свойств, упорядоченных в соответствии с эмпирически обоснованным нарастанием системной (модельной) сложности:

(1) «Базовая» модель системы:

{Элементы:{…}, структура:{…}, функции:{…}, динамические свойства:{…},

взаимодействие с внешней средой:{…}, управление:{…}, целеполагание:{…},

самоуправление:{…}, поведение:{…}, гомеостазис:{…}, самоорганизация:{…},

развитие:{…}, эволюция:{…},……, цель исследования:{…}, исследователь:{…}}.

К моделям предъявляют следующие требования [6]:

- ингерентность модели, то есть достаточная степень согласованности создаваемой модели со средой, чтобы создаваемая модель была согласована со средой, в которой ей предстоит функционировать, входила бы в эту среду не как чужеродный элемент, а как естественная составная часть[7].

- простота модели. Простота модели – ее неизбежное свойство: в модели невозможно зафиксировать все многообразие реальных ситуаций.

- адекватность модели – означает возможность с ее помощью достичь поставленной цели моделирования в соответствии со сформулированными критериями. Адекватность модели означает, в частности, что она достаточно полна, точна и устойчива. Достаточно не вообще, а именно в той мере, которая позволяет достичь поставленной цели. Иногда удается (и это желательно) ввести некоторую меру адекватности модели, то есть определить способ сравнения разных моделей по степени успешности достижения цели с их помощью.

Можно выделить следующие этапы построения математической модели(рис. 1.1).

1. Определение предмета и цели моделирования, включая границы исследуемой системы и те основные свойства, которые должны быть отражены. На этом этапе определяется предельный уровень сложности модели и во многом предопределяются результаты следующих этапов.

2. Выбор языка (аппарата) моделирования. Существует несколько сотен «аппаратов» моделирования, каждый из которых представляет собой разветвленный раздел прикладной математики.

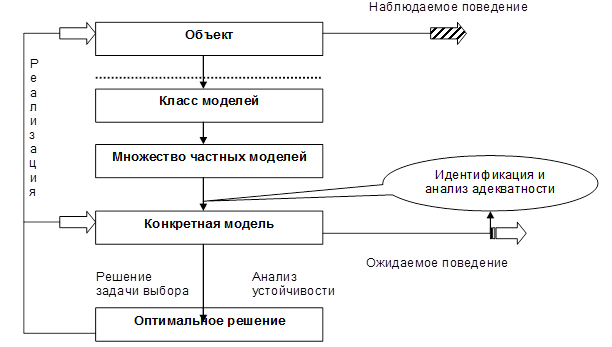
Рис. 1.1. Этапы построения и исследования математической модели

3. Выбор переменных, описывающих состояние системы и существенные параметры внешней среды, а также шкал их измерения и критериев оценки.

4. Выбор ограничений, то есть множеств возможных значений переменных и параметров, и (в динамических моделях) начальных условий.

5. Определение связей между переменными с учетом всей имеющейся информации о моделируемой системе, а также известных законов, закономерностей и т.п., описывающих данную систему. Именно этот этап иногда называют «построение модели» (в узком смысле).

6. Исследование модели – решение прямой и обратной задач моделирования. Именно этот этап иногда называют «моделированием» (в узком смысле).

7. Изучение устойчивости и адекватности модели.

Последующие этапы связаны с практической реализацией модели и/или внедрением результатов моделирования.

Приведенные этапы математического моделирования иногда приходится повторять, возвращаясь к более ранним этапам при уточнении цели моделирования, обеспечении точности, устойчивости, адекватности и т.д.