Матричные способы задания графов. Упорядочение элементов орграфа

При большом числе элементов рисунок графа теряет наглядность. В таком случае граф целесообразно задать матричным способом. Этот способ также удобен и для решения задачи на компьютере.

Определение 12.3. Матрицей инцидентности орграфа без петель с n вершинами и m дугами называется матрица, любой элемент которой определяется по следующей формуле:

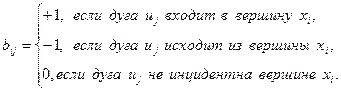
Для неориентированного графа вместо «–1» ставится «1».

Пример.Для заданного ориентированного графа (рис. 12.10) построить матрицу инцидентности:

Рис. 12.10

Матрица инцидентности орграфа:

.

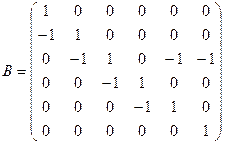Определение 12.4. Матрица смежности вершин орграфа – квадратная матрица n-го порядка (n – число вершин). Строки и столбцы матрицы соответствуют вершинам графа. Элементы S_ij матрицы равны числу дуг, направленных из i-й вершины в j-ю.

В случае неориентированного графа ему вместе с ребром (x_i,x_j) принадлежит и ребро (x_j,x_i), поэтому матрица будет симметрической.

Пример.Для заданного ориентированного графа (рис. 12.11) построить матрицу смежности вершин:

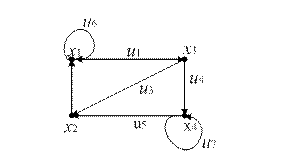
Рис 12.11

Матрица смежности вершин орграфа:

.

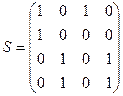Определение 12.5. Матрица смежности дуг орграфа – квадратная матрица m-го порядка (m – число дуг). Строки и столбцы матрицы соответствуют дугам графа. Элементы q_ij равны 1, если дуга u_i непосредственно предшествует дуге u_j, и нулю в остальных случаях.

Для неориентированного графа матрица смежности дуг симметрическая с элементами равными 1, если ребра имеют общую вершину, и 0 в остальных случаях.

Пример.Для заданного ориентированного графа (рис. 12.12) построить матрицу смежности дуг:

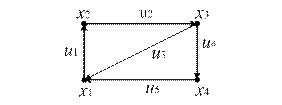
Рис.12.12

Матрица смежности дуг орграфа:

.

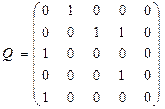Расчеты в задачах, связанных с графами, заметно упрощаются, если их элементы упорядочены.

Определение 12.6. Вершина x_i предшествует вершине x_j, если существует путь из x_i в x_j, тогда x_i называется предшествующей вершине x_j, а x_j – последующей за x_i.

Под упорядочением вершин связного орграфа без контуров понимают такое разбиение его вершин на группы, при котором:

1) вершины первой группы не имеют предшествующих, а вершины последней – последующих;

2) вершины любой другой группы не имеют предшествующих в следующей группе;

3) вершины одной и той же группы дугами не соединяются.

В результате упорядочения элементов получают граф, изоморфный данному.

Графический способ упорядочения вершин – алгоритм Фалкерсона:

1) Находят вершины графа, в которые не входит ни одна дуга. Они образуют первую группу.

2) Вершины и исходящие из них дуги исключают из дальнейшего рассмотрения (то есть вычеркивают).

3) Устанавливается следующая группа вершин, в которую не входит ни одна дуга. Этот шаг повторяют до тех пор, пока все вершины не будут упорядочены.

Пример.Упорядочить вершины орграфа (рис. 12.13):

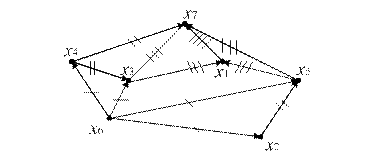
Рис. 12.13

Упорядочим вершины орграфа по алгоритму Фалкерсона (рис. 12.14):

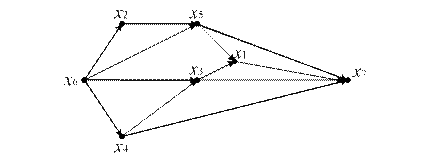
Рис. 12.14