
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общая постановка задачи динамического программирования
Определение 11.1. Динамическое программирование – это метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми.
Многие экономические процессы расчленяются на шаги естественным образом. Например, процессы планирования и управления, развиваемые во времени. Здесь естественный шаг: год, квартал, месяц и т.д.
Рассматриваемые ранее задачи (ЗЛП и ЗНП) относятся к задачам однократного принятия решений, ЗДП требует некоторой последовательности принятых решений и относится к многоэтапным (многошаговым) задачам.
Если модели линейного программирования можно использовать в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели динамического программирования применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию и т.д.
В общем случае ЗДП формулируется следующим образом: имеется некоторая управляемая система S, характеризующаяся определенным набором параметров, задающих ее состояние, которая под влиянием управления переходит из начального состояния в конечное.
Состояние системы на каждом шаге определяется вектором-состояния 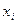 . Дальнейшее изменение ее состояния зависит только от данного состояния и не зависит от того, каким путем система перешла в него (процесс без последействия).
. Дальнейшее изменение ее состояния зависит только от данного состояния и не зависит от того, каким путем система перешла в него (процесс без последействия).
На каждом шаге выбирается одно решение 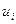 (управление), под действием которого система переходит из предыдущего состояния
(управление), под действием которого система переходит из предыдущего состояния 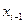 в новое
в новое 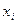 . Это новое состояние является функцией состояния на начало шага
. Это новое состояние является функцией состояния на начало шага 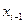 и принятого в начале решения
и принятого в начале решения 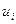 , то есть
, то есть  .
.
Действие на каждом шаге связано с определенным выигрышем (доходом, прибылью) или потерей (издержками), которые зависят от состояния на начало шага и принятого решения:
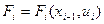 – приращение целевой функции в результате i-го шага и принятого решения:
– приращение целевой функции в результате i-го шага и принятого решения:
 – значение целевой функции при переходе системы из начального состояния в конечное за n шагов.
– значение целевой функции при переходе системы из начального состояния в конечное за n шагов.
На векторы-состояния и управления могут быть наложены ограничения, объединение которых составляет область допустимых решений 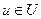 .
.
Требуется найти такое допустимое управление 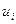 для каждого шага, чтобы получить экстремальное значение целевой функции за все n шагов.
для каждого шага, чтобы получить экстремальное значение целевой функции за все n шагов.
Определение 11.2. Любую допустимую последовательность действий для каждого шага, переводящую систему из начального состояния в конечное, называют стратегией управления. Допустимая стратегия управления, при которой целевая функция принимает экстремальное значение, называется оптимальной.
Дата добавления: 2014-12-03; просмотров: 382; Мы поможем в написании вашей работы!; Нарушение авторских прав |