
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод множителей Лагранжа. Пусть требуется решить ЗНП следующего вида
Пусть требуется решить ЗНП следующего вида
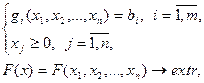
где 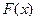 и (или)
и (или) 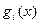 непрерывны и дифференцируемы.
непрерывны и дифференцируемы.
Для решения задачи вводят так называемую функцию Лагранжа L(x, l):
 .
.
Метод функции Лагранжа сводит ЗНП на условный экстремум к задаче нахождения локального экстремума.
Алгоритм метода:
1) Составляют функцию Лагранжа.
2) Находят стационарные точки функции Лагранжа из системы уравнений:

3) Из найденных стационарных точек выбирают те, в которых функция L(x, l) имеет локальные экстремумы. Функция L(x, l) имеет в стационарной точке локальный максимум, если в ней дифференциал второго порядка меньшего нуля (d2L<0), и локальный минимум, если дифференциал второго порядка больше нуля (d2L>0).
Множителям Лагранжа можно придать экономический смысл. Если F(x1,x2…xn) – доход, соответствующий плану x=(x1,x2…xn),  – затраты некоторых ресурсов, тогда множители
– затраты некоторых ресурсов, тогда множители 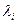 будут показывать как изменится максимальный доход, если количество ресурса i-го вида увеличится на единицу.
будут показывать как изменится максимальный доход, если количество ресурса i-го вида увеличится на единицу.
Задача.Найти условный минимум функции 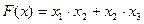 при ограничениях
при ограничениях
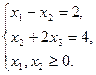
Составим функцию Лагранжа:
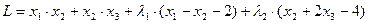 .
.
Найдем стационарные точки функции Лагранжа из системы уравнений:

Решая систему, получаем 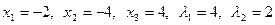 .
.
Запишем дифференциал второго порядка функции Лагранжа. Поскольку все частные производные второго порядка, в записи которых присутствуют 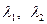 , равны нулю, то формула дифференциала второго порядка для функции Лагранжа примет вид:
, равны нулю, то формула дифференциала второго порядка для функции Лагранжа примет вид:
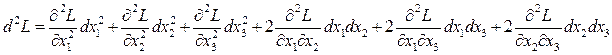 .
.
Так как 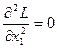 ,
, 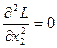 ,
, 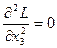 ,
,  ,
, 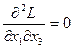 ,
, 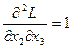 , то
, то
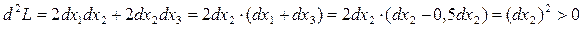 .
.
Следовательно, точка 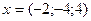 является точкой минимума функции
является точкой минимума функции 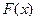 . Найдем значение функции
. Найдем значение функции 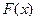 в данной точке:
в данной точке:
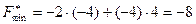 .
.
Ответ:  ,
, 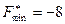 .
.
Дата добавления: 2014-12-03; просмотров: 368; Мы поможем в написании вашей работы!; Нарушение авторских прав |