Метод ветвей и границ

Алгоритм метода:

1) Отбрасывается условие целочисленности и полученная ЗЛП решается симплекс-методом.

2) Если оптимальное решение задачи удовлетворяет ограничению целочисленности, то оно является решением исходной задачи.

3) Если оптимальное решение задачи не удовлетворяет ограничению целочисленности, то множество допустимых значений разбиваем на два непересекающихся подмножества:

Квадратные скобки в новых ограничениях означают целую часть соответствующего числа.

4) Решаются полученные задачи.

5) Анализируется их решение.

6) Если оптимальный план не найден, то для дальнейшего ветвления выбирают множество с самой большой оценкой. Процесс продолжают до получения оптимального плана.

Решим сформулированную ранее ЗЦЛП методом ветвей и границ.

Оптимальное решение ЗЛП, полученное при решении ЗЦЛП методом Гомори, не удовлетворяет ограничению целочисленности, следовательно, множество допустимых значений разбиваем на два непересекающихся подмножества.

Для расщепления выберем , поскольку не имеет смысла выбирать , так как целая часть и по условию переменные неотрицательны.

Так как , то получим два непересекающихся подмножества:

и .

Преобразуем полученные ограничения к канонической форме с предпочтительными переменными, исключив базисные переменные оптимальной таблицы исходной задачи, воспользовавшись первым уравнением этой таблицы:

. .

Включим полученные уравнения в оптимальную таблицу решения ЗЛП с учетом новой базисной переменной x₅ и продолжим решение двойственным симплекс-методом.

Решение первой ветви:

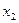
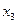
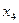
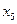
				2/5	-1/5		19/5
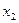
			-1/5	3/5		3/5
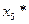
			-2/5	1/5		-4/5
			8/5*	26/5		-226/5
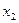
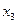
				-1/2	-5/2
						-42

Получено оптимальное целочисленное решение первой ветви задачи.

Решение второй ветви:

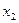
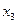
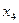
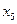
				2/5	-1/5		19/5
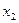
			-1/5	3/5		3/5
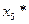
			2/5	1/5		-1/5
			8/5	26/5*		-226/5
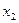
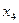
			-2		-5
						-40

Получено оптимальное целочисленное решение второй ветви задачи.

Сравнивая значения целевых функций двух ветвей решения задачи, выпишем наилучший ответ.

Ответ: , .

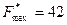Замечание 9.3. Если среди несколько дробных, то расщепляется та , дробная часть которой ближе к .

Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение решать ЗЛП с учетом дополнительных требований – целочисленности переменных.

Тема 10. Элементы нелинейного программирования

План лекции:

1. Постановка задачи нелинейного программирования (ЗНП)

2. Метод множителей Лагранжа

3. Задача выпуклого программирования

4. Задача квадратического программирования