
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача выпуклого программирования
Пусть дана система неравенств вида:

причем все функции 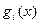 являются выпуклыми на некотором выпуклом множестве М, а функция
являются выпуклыми на некотором выпуклом множестве М, а функция 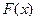 либо выпукла вверх (выпукла), либо выпукла вниз (вогнута) на множестве М.
либо выпукла вверх (выпукла), либо выпукла вниз (вогнута) на множестве М.  ЗВП состоит в отыскании такого решения системы ограничений, при котором выпуклая функция
ЗВП состоит в отыскании такого решения системы ограничений, при котором выпуклая функция 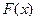 достигает минимального значения, или вогнутая функция
достигает минимального значения, или вогнутая функция 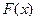 достигает максимального значения.
достигает максимального значения.
Определение 10.1. Точка (x*, λ*) называется седловой точкой функции Лагранжа, если n-мерная точка x* является точкой минимума функции L(x, λ*), а m-мерная точка λ* – точкой максимума функции L(x*, λ), так что 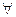 x и λ выполняется неравенство:
x и λ выполняется неравенство:
 .
.
Теорема 10.1. (Условие регулярности Слейтера) Множество Х допустимых решений ЗВП удовлетворяет условию регулярности Слейтера, если существует по крайне мере одно точка 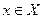 , такая что
, такая что  .
.
Теорема 10.2 (теорема Куна-Таккера). Чтобы точка x* была оптимальным решением ЗВП, множество допустимых решений которой обладают свойством регулярности Слейтера, необходимо и достаточно, чтобы существовала такая пара (x*, λ*), которая являлась бы седловой точкой функции Лагранжа данной ЗВП.
Замечание 10.1. Если ограничения задачи – линейные функции, то выполнение условия регулярности не требуется.
Для того чтобы найти седловые точки необходимо и достаточно составить систему:



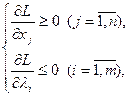
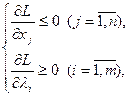

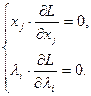
Дата добавления: 2014-12-03; просмотров: 290; Мы поможем в написании вашей работы!; Нарушение авторских прав |