Задача квадратического программирования

Одним из частных видов ЗВП является задача, в которой целевая функция содержит квадратичное слагаемое, а ограничения носят линейный характер. Такая задача относиться к квадратичному программированию.

В качестве основной в квадратичном программировании рассматривается задача минимизации функции

,

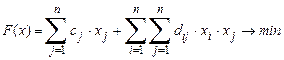при ограничениях .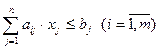

Далее будем считать, что решаемая задача квадратичного программирования является частным случаем ЗВП.

Функция Лагранжа в данном случае имеет вид:

.

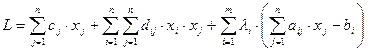Найдем стационарные точки функции Лагранжа:

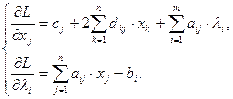
С учетом ориентации и применяя теорему Куна-Таккера:

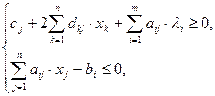(10.1)

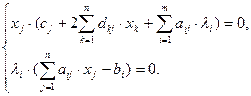(10.2)

Преобразуем систему (10.1) к системе уравнений:

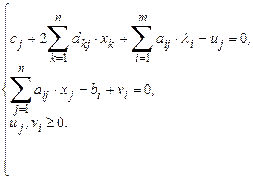
Отсюда:

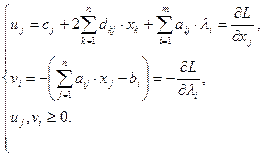
Тогда систему уравнений (10.2) можно записать в виде:

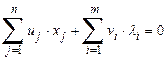. (10.3)

Чтобы учесть условие (10.3) при решении ЗНП надо следить за тем, чтобы среди базисных переменных не было u и x с одним и тем же индексом, аналогично λ и v.

Далее задача решается методом искусственного базиса.

Задача.Минимизировать функцию 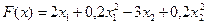при ограничениях:

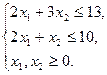
Составим функцию Лагранжа:

.

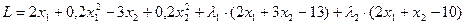Составим локальные условия Куна-Таккера:

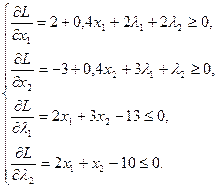
Преобразуем полученную систему ограничений к допустимому виду канонической формы:

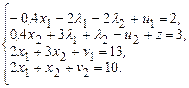
Далее решаем задачу методом искусственного базиса, учитывая условие (10.3):

N	б.п.	x1	x2	λ1	λ 2	u1	u2	v1	v2	z	b
	u1	-0,4		-2	-2
z		0,4				-1
v1*
v2
G		-0,4*	-3	-1
	u1	-0,4		-2	-2
z*	-4/15					-1	-2/15			19/15
x2	2/3						1/3			13/3
v2	4/3						-1/3			17/3
G	41/5		-3*	-1			2/15			19/15
	u1										128/45
λ1	-4/45			1/3		-1/3	-2/45		1/3	19/45
x2	2/3						1/3			13/3
v2	4/3						-1/3			17/3
G

Получили оптимальный план решения задачи 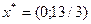. Найдем значение целевой функции в данной точке:

.

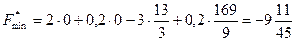Ответ: , .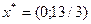

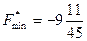Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение использовать аналитические методы решения задач математического программирования при наличии нелинейных функциональных зависимостей экономических переменных.

Тема 11. Метод динамического программирования

План лекции:

1. Общая постановка задачи динамического программирования (ЗДП)

2. Принцип оптимальности. Функциональные уравнения Беллмана

3. Задача оптимального распределения инвестиций

4. Задача о замене оборудования