Метод дифференциальных рент

При решении ТЗ методом дифференциальных рент наилучшим образом распределяют часть продукции между потребителями и на последующих итерациях постоянно уменьшают общую величину нераспределенных поставок.

Алгоритм метода:

1) В каждом столбце определяется минимальный тариф и соответствующая клетка помечается.

2) Отмеченные клетки заполняются максимально возможными поставками.

3) Оцениваются поставщики:

а) строки, соответствующие поставщикам, запасы которых неисчерпаны, являются положительными;

б) строки, соответствующие поставщикам, запасы которых исчерпаны, а потребности отмеченных потребителей неудовлетворены (с учетом всего столбца), являются отрицательными;

в) строки, соответствующие поставщикам, запасы которых исчерпаны, а потребности отмеченных потребителей удовлетворены (с учетом всех заполненных клеток столбца), имеют нулевую оценку; при этом, если заполненная клетка в нулевой строке связана через столбец с заполненной клеткой в отрицательной строке, то данная нулевая строка считается отрицательной, во всех других случаях – положительной.

4) Для каждого столбца, имеющего отмеченный тариф в отрицательной строке, находится разность между отмеченным тарифом и минимальным по величине тарифом, стоящим в положительной строке (может быть отмеченным).

5) Среди полученных разностей, отличных от 0, определяется минимальная. Это число называется промежуточной рентой.

6) Строится новая таблица, при этом тарифы, стоящие в положительных строках, переписываются без изменения, а тарифы, стоящие в отрицательных строках, увеличиваются на величину промежуточной ренты.

7) Переход к пункту 1.

Замечание 8.2. Если в строке или столбце окажется более одной выделенной клетки, то заполняются в первую очередь выделенные клетки, которые являются единственными в строке или столбце.

Замечание 8.3. Если удается распределить все запасы, то получен оптимальный план.

Замечание 8.4. При расчете оптимальной целевой функции необходимо вернуться к тарифам исходной таблицы, так как в последующих таблицах тарифы испорчены дифференциальными рентами.

Решим сформулированную ранее ТЗ методом дифференциальных рент. Построим следующие итерационные таблицы по указанному алгоритму:

					оценка
					-140
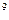
					+20
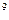
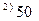
					+120
рента	-	-

					оценка
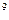
					-20
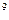
					+20
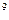
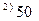
					-0
рента	-

					оценка
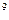
рента	-	-	-	-

В последней итерации удалось распределить все запасы, следовательно, получен оптимальный план.

Рассчитаем оптимальное значение целевой функции задачи .

Ответ: , .