
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение ТЗ методом потенциалов
Сущность метода: сначала находят опорный план решения задачи, а затем последовательно улучшают его до тех пор, пока не будет получен оптимальный план. Существует несколько способов построения опорного плана.
Определение 8.1. Опорный план называется невырожденным, если количество заполненных клеток равно n + m – 1.
Задача. Решить ТЗ, заданную следующей таблицей:

| ||||

| 
| 
| 
| |

| 
| 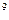
| 
| |
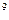
| 
| 
| 
|
Так как  и
и 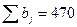 , то модель ТЗ закрытая.
, то модель ТЗ закрытая.
1) Метод северо-западного угла.
Метод позволяет за n+m–1 шаг заполнить клетки таблицы таким образом, чтобы удовлетворить все потребности, исчерпав при этом все запасы. Заполнение клеток таблицы начинается с левой верхней клетки для  и заканчивается клеткой
и заканчивается клеткой  .
.
Получим опорное решение по методу северо-западного угла, заполнив таблицу:

| ||||

| 
| 
| 
| |

| 
| 
| 
| |
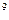
| 
| 
| 
|
Получен невырожденный план, так как число заполненных клеток равно 6, что совпадает со значением выражения n+m–1=4+3–1=6.
Определим значение целевой функции для данного плана решения задачи 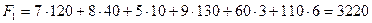 .
.
2) Метод минимального элемента.
Последовательно заполняются клетки с наименьшей стоимостью перевозок. Если имеется несколько клеток с наименьшей стоимостью, то из них выбирается любая. Клетка заполняется максимально возможным числом, при этом исчерпываются либо запасы, либо потребности.
Найдем опорное решение по методу минимального элемента, заполнив таблицу:

| ||||

| 
| 
| 
| |

| 
| 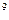
| 
| |
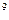
| 
| 
| 
|
Получен невырожденный план.
Значение целевой функции для данного плана решения задачи  .
.
3) Метод аппроксимации Фогеля.
В таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Наибольшая разность помечается кружком О. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейший расчет не принимаются. На каждом этапе заполняется только одна клетка.
Найдем опорное решение по методу аппроксимации Фогеля, заполнив таблицу:

| ||||||||

| 
| 
| 
| |||||

| 
| 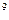
| 
| |||||
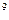
| 
| 
| 
| |||||
Получен невырожденный план.
Значение целевой функции для данного плана решения задачи  .
.
Как правило, при построении опорного плана вышеуказанными методами выполняется соотношение  .
.
Замечание 8.1. При нахождении начального опорного плана перевозок возможен случай вырождения, когда в результате вычислений значения поставки получается, что потребности в пункте удовлетворены, а запасы в пункте исчерпаны. Тогда одновременно из рассмотрения выбывают строка и столбец. В этом случае рекомендуется осуществить в одну из клеток выбывающих строки и столбца (в клетку с наименьшей стоимостью) так называемую нулевую поставку. Клетка с такой поставкой считается заполненной.
Проверка плана на оптимальность
Теорема 8.1. Если для некоторого опорного плана ТЗ существуют числа 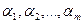 (потенциалы поставщиков) и числа
(потенциалы поставщиков) и числа  (потенциалы потребителей), такие что
(потенциалы потребителей), такие что  (8.1) для
(8.1) для  (клетка заполнена) и
(клетка заполнена) и  (8.2) для
(8.2) для  (клетка пуста)
(клетка пуста)  , то план является оптимальным.
, то план является оптимальным.
Для заполненных клеток составляется система, которая содержит n+m–1 уравнение и n+m неизвестных. Поэтому полагается, что 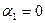 , а затем находятся остальные переменные.
, а затем находятся остальные переменные.
Для свободных клеток определяются числа  . Если
. Если  , то условия теоремы выполнены, план оптимален. Если же
, то условия теоремы выполнены, план оптимален. Если же  , то план не оптимален, и его следует улучшить.
, то план не оптимален, и его следует улучшить.
Проверим на оптимальность план, полученный по методу минимального элемента:

| 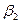
| 
| 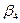
| ||

| |||||

| 
| 
| 
| 
| |

| 
| 
| 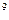
| 
| |

| 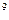
| 
| 
| 
|
Для  составим систему уравнений:
составим систему уравнений:
 ,
,
 , Пусть
, Пусть 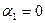 ,
,  =0,
=0,
 ,
,  = -4,
= -4, 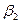 =0,
=0,
 ,
,  =-2 ,
=-2 ,  =1,
=1,
 ,
, 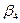 =4.
=4.
 .
.
Для  подсчитаем значения выражений:
подсчитаем значения выражений:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Так как получена положительная разность  , то план не оптимален.
, то план не оптимален.
Дата добавления: 2014-12-03; просмотров: 268; Мы поможем в написании вашей работы!; Нарушение авторских прав |