
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоремы теории игр для парных матричных игр с нулевой суммой
Теорема 6.1. (Основная теорема ТИ) Всякая конечная игра имеет цену, и у каждого игрока существует, по крайней мере, одна оптимальная стратегия.
Теорема 6.2. В матричной игре нижняя цена игры не превосходит верхней цены игры, то есть  , а для цены игры с справедливо: a £ с £ b.
, а для цены игры с справедливо: a £ с £ b.
Определение 6.4. Смешанной стратегией первого (второго) игрока называется вектор 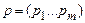 , где
, где  и
и  , (
, (  , где
, где  и
и 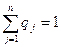 ).
).
Теорема 6.3. Игра с седловой точкой имеет оптимальное решение в чистых стратегиях.
Теорема 6.4. (Теорема Неймана) Всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях, если чистую стратегию считать частным случаем смешанной, когда одна вероятностная компонента равна 1, а остальные – нулю.
Теорема 6.5. Для того чтобы смешанные стратегии  и
и  были оптимальными для игроков А и В в игре с платежной матрицей
были оптимальными для игроков А и В в игре с платежной матрицей  и выигрышем с, необходимо и достаточно выполнение неравенств:
и выигрышем с, необходимо и достаточно выполнение неравенств:
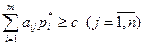 – сложение по столбцу,
– сложение по столбцу,
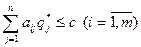 – сложение по строке.
– сложение по строке.
То есть первый игрок, придерживаясь своей оптимальной стратегии  , не может выиграть меньше с, второй игрок, придерживаясь своей оптимальной стратегии
, не может выиграть меньше с, второй игрок, придерживаясь своей оптимальной стратегии  , не позволит первому выиграть больше с.
, не позволит первому выиграть больше с.
Данная теорема дает ответ на вопрос о существовании решения игры и определяет путь решения.
Теорема 6.6. (Об активных стратегиях) Если игроки придерживаются своих активных стратегий, то выполняется следующая система уравнений:
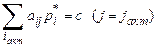 – сложение по столбцу активной стратегии,
– сложение по столбцу активной стратегии,
 – сложение по строке активной стратегии.
– сложение по строке активной стратегии.
Теорема 6.7. Оптимальные смешанные стратегии  и
и  соответственно игроков А и В в матричной игре с платежной матрицей
соответственно игроков А и В в матричной игре с платежной матрицей  с ценой с будут оптимальными и в матричной игре с платежной матрицей
с ценой с будут оптимальными и в матричной игре с платежной матрицей  с ценой игры
с ценой игры  , где b>0.
, где b>0.
3. Способы решения задач ТИ:
1) Простейшими из матричных игр являются игры  ,
, 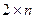 и
и 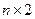 . Использование теоремы 6.6 для таких игр составляет первый способ решения.
. Использование теоремы 6.6 для таких игр составляет первый способ решения.
Пример 1. Найти решение игры, заданной матрицей:
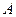
 .
.
Решение:
1) Найдем нижнюю и верхнюю цену игры:
 ,
,
 .
.
Следовательно,  . Так как
. Так как  , то игра не является игрой с седловой точкой и решение следует искать в смешанных стратегиях.
, то игра не является игрой с седловой точкой и решение следует искать в смешанных стратегиях.
2) Пусть  и
и  – оптимальные смешанные стратегии первого и второго игроков соответственно. Тогда по теореме 6.6 получим системы:
– оптимальные смешанные стратегии первого и второго игроков соответственно. Тогда по теореме 6.6 получим системы:
 и
и 
Решим первую систему. Вычитая из первого второе уравнение системы, получим  или
или  . Подставив это соотношение в третье уравнение, будем иметь
. Подставив это соотношение в третье уравнение, будем иметь  , откуда
, откуда  . Следовательно,
. Следовательно, 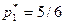 . Цену игры можно найти, если подставить полученные значения
. Цену игры можно найти, если подставить полученные значения 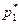 и
и 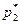 в одно из первых уравнений системы. Так, согласно первому уравнению
в одно из первых уравнений системы. Так, согласно первому уравнению 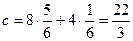 .
.
Аналогично получаем решение второй системы:
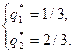
Ответ:  ,
,  , с=22/3.
, с=22/3.
2) Графический способ решения матричных игр  ,
, 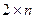 и
и 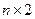 .
.
Пример 2. Найти решение игры, заданной матрицей:
 .
.
Решение:
1) Найдем нижнюю и верхнюю цену игры:
 ,
,
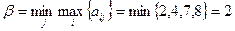 .
.
Следовательно,  .
.
2) Изобразим стратегии игроков на плоскости pОq (рис. 6.1). Горизонтальной выбирается та ось, которая соответствует игроку с двумя стратегиями. На горизонтальной оси Оp выбирается отрезок  . Из точек 0 и 1 восстановим перпендикуляры и на них отложим выигрыши первого игрока при использовании вторым игроком своих возможных стратегий. Соединим соответствующие точки на перпендикулярах прямыми:
. Из точек 0 и 1 восстановим перпендикуляры и на них отложим выигрыши первого игрока при использовании вторым игроком своих возможных стратегий. Соединим соответствующие точки на перпендикулярах прямыми:  . Точки этих прямых будут соответствовать средним выигрышам первого игрока при использовании некоторой смешанной стратегии.
. Точки этих прямых будут соответствовать средним выигрышам первого игрока при использовании некоторой смешанной стратегии.

Рис. 6.1
Нижняя ломаная соответствует среднему гарантированному выигрышу. Вершина ломаной - максимальный гарантированный выигрыш. Следовательно, цена игры и оптимальные стратегии определяются  и
и  .
.
3) Составим уравнения этих прямых и определим цену игры с и смешанные стратегии:
 и
и 
Ответ:  ,
,  , с=7/4.
, с=7/4.
Замечание 6.1. При решении игры, заданной матрицей 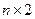 , минимально удаленная от оси q точка верхней ломанной (ограничивающей максимальные средние выигрыши первого игрока) соответствует минимально возможному проигрышу второго игрока для оптимальных смешанных стратегий обоих игроков.
, минимально удаленная от оси q точка верхней ломанной (ограничивающей максимальные средние выигрыши первого игрока) соответствует минимально возможному проигрышу второго игрока для оптимальных смешанных стратегий обоих игроков.
3) Вышеуказанные способы решения задач ТИ имеют ограничение на использование. Способ сведения задачи ТИ к ЗЛП по теореме 6.5 лишен этого недостатка.
Задача.Предприятие может выпускать два вида продукции  , получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний
, получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний  . Дана матрица
. Дана матрица  , элементы которой характеризуют прибыль, которую получит предприятие при выпуске i-й продукции при j-м состоянии спроса. Определить оптимальные пропорции в выпускаемой продукции с помощью линейного программирования, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.
, элементы которой характеризуют прибыль, которую получит предприятие при выпуске i-й продукции при j-м состоянии спроса. Определить оптимальные пропорции в выпускаемой продукции с помощью линейного программирования, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.
Решение задачи:
Упростим платежную матрицу, отбросив стратегии заведомо невыгодные или дублирующие. Так, вторая стратегия (второй столбец) является явно невыгодной по сравнению с первой (элементы второго столбца больше элементов первого столбца), так как цель игрока В – уменьшить выигрыш игрока А. Поэтому второй столбец можно отбросить. Получим матрицу  .
.
Замечание 6.2. Если в платежной матрице элементы k-той строки не меньше соответствующих элементов s-той, s-тая строка вычеркивается.
Замечание 6.3. Если элементы l-того столбца не превосходят соответствующих элементов r-того столбца, то r-тый столбец вычеркивается.
Найдем нижнюю и верхнюю цену игры:
 ,
,
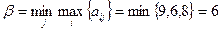 .
.
Следовательно,  .
.
Согласно теореме 6.5 о цене игры 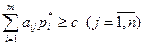 и
и 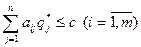 . Пусть для определенности с>0. Разделим каждое неравенство на с:
. Пусть для определенности с>0. Разделим каждое неравенство на с:
 и
и  .
.
Обозначив  (6.1) и
(6.1) и  (6.2) и приняв во внимание, что первый игрок стремится по возможности увеличить цену игры, тогда как второй – уменьшить ее величину, и так как
(6.2) и приняв во внимание, что первый игрок стремится по возможности увеличить цену игры, тогда как второй – уменьшить ее величину, и так как  и
и 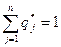 , то
, то
 .
.
В результате получим пару взаимно двойственных задач:
 и
и  .
.
Решив одну из этих задач, получим решение другой. Решать удобнее ту задачу, в которой число столбцов больше числа строк. При этом необходимо выполнить обратный переход:
 ,
,  ,
,  . (6.3)
. (6.3)
Вернемся к решению поставленной задачи. По матрице игры 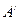 составим пару двойственных задач линейного программирования:
составим пару двойственных задач линейного программирования:
 и
и 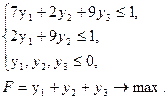
Решим вторую задачу основным симплекс-методом, предварительно преобразовав математическую модель задачи к канонической форме с предпочтительными переменными:

| 
| 
| 
| 
| 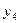
| 
| 
|
 * *
| |||||||

| |||||||

| -1* | -1 | -1 | ||||
| 2/7 | 9/7 | 1/7 | 1/7 | |||
 * *
| 59/7 | -18/7 | -2/7 | 5/7 | |||

| -5/7* | 2/7 | 1/7 | -1/7 | |||

| 49/413 | ||||||
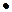 
| -18/59 | -2/59 | 7/59 | 5/59 | |||

| 28/413 | 49/413 | 5/59 | -84/413 |
Получили оптимальный план решения второй задачи:  ,
, 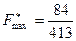 . Тогда, используя соответствие между переменными исходной и двойственной задач, выпишем оптимальное решение первой задачи:
. Тогда, используя соответствие между переменными исходной и двойственной задач, выпишем оптимальное решение первой задачи:  ,
,  .
.
По формуле 6.3 получим цену игры  .
.
Используя формулы 6.1 и 6.2, получим оптимальные смешанные стратегии игроков:
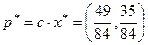 и
и  .
.
Ответ:  ,
,  ,
,  .
.
Таким образом, в ответе указаны оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли  при любом состоянии спроса.
при любом состоянии спроса.
Педагогический комментарий.Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение вырабатывать компромиссные рекомендации при конфликтных ситуациях принятия решения.
Тема 7. Матричные статистические игры
План лекции:
1. Понятие статистической игры
2. Критерии выбора оптимальной стратегии при решении
статистической игры
3. Кооперативные игры
Дата добавления: 2014-12-03; просмотров: 361; Мы поможем в написании вашей работы!; Нарушение авторских прав |