Суть симплексного метода

Для использования симплекс-метода ЗЛП должна быть приведена к каноническому виду с предпочтительными переменными.

Критерий оптимальности. Решение ЗЛП является оптимальным, если неотрицательны коэффициенты целевой функции при переменных, имеющих определенный смысл (экономический, технологический, физический), и все свободные члены в правой части уравнений системы ограничений ( ).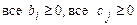

В ходе решения ЗЛП могут возникнуть 4 случая:

1) 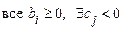, следовательно, план не оптимален и используется основной симплекс-метод;

2) 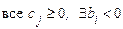, следовательно, план не оптимален и применяется двойственный симплекс-метод;

3) 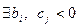, следовательно, план не оптимален и применяется смешанный симплекс-метод;

4) 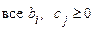, следовательно, согласно критерию оптимальности, план оптимален.

3. Алгоритм основного симплекс-метода:

1) Записать математическую модель в допустимом предпочтительном виде канонической формы.

2) Составить нулевую итерацию, записав математическую модель ЗЛП в первую симплекс-таблицу и взяв в качестве базисных переменных предпочтительные.

3) При наличии отрицательных коэффициентов целевой функции с_j осуществить подготовку к переходу к новому решению по следующей схеме:

а) среди отрицательных коэффициентов целевой функции 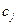выбрать максимальный по модулю, соответствующий столбец в симплекс-таблице называется разрешающим и помечается знаком *.

б) среди всех отношений правых частей 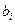системы ограничений к положительным элементам разрешающего столбца выбрать минимальное, соответствующая строка называется разрешающей и помечается знаком *.

в) элемент, стоящий на пересечении разрешающего столбца и разрешающей строки, называется разрешающим и помещается в рамку .

4) Заполнить следующую симплекс-таблицу:

а) базисную переменную (б.п.) в разрешающей строке заменить на переменную разрешающего столбца, все остальные переменные оставить в неизменном порядке;

б) заполнить столбцы базисных переменных: на пересечении столбца и строки базисной переменной поставить 1, остальные элементы столбца приравнять нулю;

в) если в разрешающем столбце прежней таблицы есть 0, то соответствующую ему строку переписать без изменений;

г) если в разрешающей строке прежней таблицы есть 0, то соответствующий ему столбец переписать без изменений;

д) построить опорную строку (·) в новой таблице, разделив все элементы разрешающей строки прежней таблицы на разрешающий элемент;

е) все остальные элементы новой таблицы определяются по правилу треугольника: новый элемент равен прежнему минус произведение соответствующего по строке элемента в разрешающем столбце прежней таблицы на элемент опорной строки в столбце искомого элемента новой таблицы; исключением является элемент, стоящий на пересечении строки целевой функции и столбца свободных членов ограничений, для которого в правиле треугольника "–" следует заменить на "+".

5) Целевая функция в новой таблице проверяется на оптимальность: если 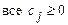при реальных переменных, то получен оптимальный план решения ЗЛП, а если среди с_j есть отрицательный коэффициент, то перейти к пункту 2 алгоритма.

Задача.Для изготовления двух видов 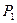, 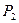продукции используют три вида ресурсов 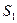, , . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в технологической таблице:

Вид ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции	Объем ресурса
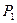
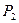
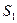
Прибыль от реализации единицы продукции, ден. ед.

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение задачи:

Введем обозначения: х₁ – количество продукции первого вида, х₂ – количество продукции второго вида. Тогда экономико-математическая модель задачи примет вид:

.

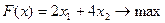Преобразуем математическую модель ЗЛП к допустимому предпочтительному виду канонической формы:

.

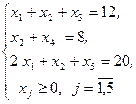
По алгоритму основного симплекс-метода заполним симплексную таблицу задачи:

	б.п.
*
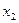
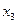
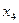
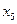
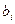
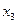
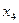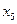
	F	–2	–4*
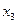	*				–1
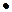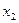
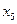
				–1
	F	–2*					–32
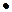
					–1
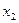
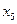
			–2
	F						–40

Итак, получили, что 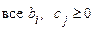. Следовательно, согласно критерию оптимальности, план оптимален.

Ответ: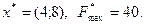

Таким образом, для получения максимальной прибыли в размере 40 ден. ед. надо продать 4 изделия первого вида и 8 изделий второго вида.

4. Алгоритм двойственного симплекс-метода:

1) Записать математическую модель ЗЛП в предпочтительном виде канонической формы.

2) В симплекс-таблице среди отрицательных свободных членов 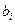системы ограничений выбрать максимальный по модулю, соответствующая строка называется разрешающей и помечается *.

3) Среди всех отношений коэффициентов целевой функции к отрицательным элементам разрешающей строки выбрать минимальное по модулю, соответствующий столбец называется разрешающим и помечается знаком *.

4) Выполнить переход к новой симплекс-таблице по алгоритму основного симплекс-метода.

5. Алгоритм смешанного симплекс-метода:

1) Записать математическую модель ЗЛП в предпочтительном виде канонической формы.

2) Начать решение ЗЛП основным симплекс-методом, то есть уравнения с отрицательными свободными коэффициентами 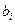системы ограничений при определении разрешающей строки не рассматривать на этом этапе. Другими словами, базисные переменные в уравнениях с отрицательными 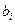нельзя выводить из базиса на этом этапе. Задача решается основным симплекс-методом до тех пор, пока в строке целевой функции не будет отрицательных элементов.

3) Если после этого в столбце свободных элементов остались отрицательные, то решение продолжить по алгоритму двойственного симплекс-метода.

6. Особые случаи симплекс-метода:

1) Не единственность оптимального решения (альтернативный оптимум): если в оптимальной симплекс-таблице в строке целевой функции имеется хотя бы один нулевой коэффициент c_j при соответствующей свободной переменной, то ЗЛП имеет бесконечное множество оптимальных решений.

2) Появление вырожденного базисного решения может привести к "зацикливанию", то есть возвращению к ранее найденному ДБР, и в этом случае процесс решения ЗЛП становится бесконечным. Методы выхода: изменение выбора разрешающего столбца, разрешающей строки и т.д.

3) Отсутствие оптимума (несовместность системы ограничений): система не имеет решения в том случае, если невозможно выбрать разрешающую строку или столбец из-за отсутствия удовлетворяющих алгоритмам симплекс-методов элементов.

4) Неограниченность решения: в некоторых задачах линейного программирования значения переменных могут неограниченно увеличиваться без нарушения ограничений. Следовательно, пространство допустимых решений не ограничено, по крайней мере, по одному направлению. В результате этого целевая функция может возрастать или убывать неограниченно. Это говорит о том, что модель задачи разработана не достаточно корректно.

Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение выполнять оптимизационные расчеты и экономически интерпретировать полученные результаты на основе универсального симплекс-метода решения задачи линейного программирования.

Тема 4. Модифицированный симплекс-метод решения ЗЛП. Устойчивость оптимального решения ЗЛП

План лекции:

1. Обращенный базис и симплекс-множители

2. Алгоритм модифицированного симплекс-метода

3. Устойчивость оптимального решения ЗЛП