КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Абуева Н.С.
А13 Математическое программирование: Курс лекций: Учебное пособие для студентов 2-го курса экономических специальностей / Под ред. И.Л. Макаровой. – Сочи: СГУТиКД, 2007. – 123 с.: табл.
Пособие содержит определения, правила, алгоритмы, теоремы и формулы, необходимые для решения задач по математическому программированию. Излагаются методы решения задач линейного программирования, транспортной задачи, элементы теории двойственности, матричных игр, рассматриваются дискретное, нелинейное, динамическое программирование, программирование на сетях. Приводится достаточное количество задач экономического содержания с решениями.
Для студентов экономических специальностей высших учебных заведений.
© СГУТиКД, 2007
© Абуева Н.С., 2007
оглавление
Предисловие..………………………………………..………………….……………4
Тема 1. Математическая модель задачи линейного
программирования (ЗЛП)...........................................................................................7
Тема 2. Графический метод решения ЗЛП. Закономерности и общие
свойства решения ЗЛП……………………………………………………………..14
Тема 3. Симплексный метод решения ЗЛП………………………………………23
Тема 4. Модифицированный симплекс-метод решения ЗЛП. Устойчивость
оптимального решения ЗЛП……………………………………………………….29
Тема 5. Двойственность в линейном программировании……………………….42
Тема 6. Элементы теории матричных игр………………………………………...49
Тема 7. Матричные статистические игры………………………………………...58
Тема 8. Транспортная задача………………………………………………………64
Тема 9. Дискретное программирование…………………………………………..77
Тема 10. Элементы нелинейного программирования……………………………84
Тема 11. Метод динамического программирования……………………………..91
Тема 12. Программирование на сетях…………………………………………...101
Тема 13. Планирование на сетях…………………………………………………115
Литература…………………………………………………………………………122
ПРЕДИСЛОВИЕ
Учебное пособие представляет собой курс лекций по разделу математики «Математическое программирование» для экономических специальностей (080109 «Бухгалтерский учет, анализ и аудит», 080504 «Государственное и муниципальное управление», 080507 «Менеджмент организации», 080102 «Мировая экономика», 080105 «Финансы и кредит», 080502 «Экономика и управление на предприятии») в объеме одного семестра в соответствии с Государственным образовательным стандартом высшего профессионального образования (2000 г.).
Данное учебное пособие представляет собой теоретический материал практической направленности по разделу курса математики «Математическое программирование» для экономических специальностей и является необходимой составной частью достижения цели проводимого исследования по теме «Формирование специальных профессиональных умений студентов-экономистов на занятиях по математическим дисциплинам», ведущей идеей которого является содержательное методическое изменение деятельности преподавателя и студентов-экономистов на занятиях по математическим (непрофильным) дисциплинам с целью формирования и совершенствования профессиональных знаний и умений будущих специалистов в области экономики.
Экономические проблемы, возникающие перед специалистами, в своем большинстве, зависят от множества различных, иногда противоречащих друг другу факторов, изменяются с течением времени и влияют на другие проблемы и процессы. Вследствие этого исследование экономической проблемы целесообразно проводить на адекватной математической модели. Математическая модель отражает проблему в абстрактной форме и позволяет учесть большое число разнообразных характеристик, от которых зависит эта проблема. Анализ и расчет математической модели позволяют выбрать оптимальные решения поставленной задачи и обосновать этот выбор.
Данное учебное пособие посвящено изложению построения математических моделей, методов расчета и их применению для решения экономических задач. На многочисленных примерах подробно и доступно объяснены математические методы расчета представленных моделей.
В каждой теме в популярной форме даны общая постановка задачи, построение для нее математической модели и методы ее расчета. Представлены экономические проблемы, оптимальное решение которых становится возможным после использования соответствующей математической модели. Это задачи о наилучшем использовании ресурсов, транспортная задача, задачи нахождения оптимальной стратегии, оптимального планирования инвестиций и целый ряд других.
В темах 1-5 рассмотрены модели линейного программирования – постановка и примеры типовых задач, теоретические основы, теория двойственности, симплексный и графический методы решения задач. Темы 6, 7 посвящены рассмотрению решения задач теории парных матричных игр и матричных статистических игр, тема 8 – решению транспортных задач различными методами. В теме 9 представлены методы целочисленного линейного программирования. В теме 10 описываются классические методы оптимизации задач нелинейного программирования. Тема 11 рассматривает модели задач динамического программирования, используемые при решении таких актуальных задач, как задача об оптимальном распределении средств между предприятиями, задача о замене оборудования. Темы 12 и 13 включают в себя элементы теории графов, сетевого планирования и управления.
В конце каждой темы представлен список профессиональных умений студентов-экономистов, формирование которых возможно и целесообразно на данном занятии.
Для усвоения студентами материала пособия не требуется специальных знаний по математике кроме тех, которые входят в программу подготовки студентов экономического профиля, а именно: линейная алгебра, аналитическая геометрия на плоскости, математический анализ, теория вероятностей и математическая статистика.
Поскольку выпускники вузов по экономическим специальностям в последующей практической деятельности будут встречаться с математическими методами оптимизации, главным образом, как пользователи, а не разработчики, в данном пособии основное внимание уделяется приложениям математических методов в экономике, а не их подробному теоретическому обоснованию. По этой причине в пособии приводится достаточное количество содержательных примеров, иллюстрирующих приемы математического моделирования экономических ситуаций с последующим экономическим анализом полученных результатов.
ТЕМА 1. Математическая модель задачи линейного программирования (ЗЛП)
План лекции:
1. Предмет математического программирования (МП)
2. Математическая модель задачи МП
3. Основные виды задач МП
4. Многокритериальная оптимизация
5. Основные понятия теории оптимизации
6. Постановка ЗЛП. Различные формы записи ее математической
модели
1. Предмет математического программирования
Определение 1.1. Математическое программирование – раздел математики по моделированию задач на оптимизацию функций многих переменных параметров, где существенную роль играют ограничения на область возможного изменения этих параметров.
Исследование большинства процессов, в том числе и экономических, обычно начинается с их математического моделирования, то есть отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему взаимосвязей и ограничений. В этих соотношениях выделяются такие переменные, меняя которые, можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «Математическое программирование» или «Математические методы исследования операций». Методами МП решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразовании, транспортные задачи и т.д.
2. Математическая модель МП
Определение 1.2. Математическая модель – система математических соотношений, приближенно, в абстрактной форме описывающих изучаемый процесс или систему.
Математическая модель МП устанавливает математические соотношения между переменными системы с целью определения их оптимальных значений в соответствии с условиями задачи.
Математическая модель МП включает:
1) совокупность управляемых n-переменных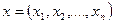 
, называемых планом задачи; вектором управления, решения; управлением, стратегией;
2) целевую функцию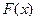 
, определяющую результирующие показатели и являющуюся критерием эффективности решения задачи (функция цели, показатель эффективности, критерий оптимальности, функционал задачи):
;
3) систему ограничений на переменные в соответствии с имеющимися ресурсами (материальными, финансовыми, трудовыми):
.
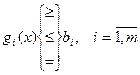Определение 1.3. Область допустимых решений (ОДР) – интервалы значений переменных 
, удовлетворяющих системе ограничений математической модели ЗЛП.
3. Основные типы задач МП:
1) Если целевая функция 
и функции 
линейны относительно переменных 
, то такая задача является задачей линейного программирования.
2) Если, исходя из содержательного смысла, решения ЗЛП должны быть целыми числами, то эта задача целочисленного линейного программирования.
3) Если критерий эффективности и (или) система ограничений, задаются нелинейными функциями, то получаем задачу нелинейного программирования. В частности, если указанные функции обладают свойствами выпуклости, то полученная задача является задачей выпуклого нелинейного программирования.
4) Если параметры целевой функции и (или) системы ограничений изменяются во времени или состоит из нескольких функций или процесс принятия решения имеет многошаговый характер, то задача относится к динамическому программированию.
5) Если параметры, входящие в целевую функцию , или ограничения задачи являются случайными, недостоверными, или если приходится принимать решения в условиях риска, неполной или недостоверной информации, то задача относится к стохастическому программированию.
Дата добавления: 2014-12-03; просмотров: 130; Мы поможем в написании вашей работы!; Нарушение авторских прав |