
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм решения ЗЛП графическим методом
Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок её графического решения:
1) С учетом системы ограничений строится ОДР: записывают уравнения прямых, соответствующих ограничениям ЗЛП, и строят их на плоскости  ; выбирают полуплоскости для каждого ограничения; определяют ОДР как область пересечения m полуплоскостей, соответствующих m ограничениям задачи.
; выбирают полуплоскости для каждого ограничения; определяют ОДР как область пересечения m полуплоскостей, соответствующих m ограничениям задачи.
2) Строится градиент  с точкой приложения в начале координат.
с точкой приложения в начале координат.
3) Проводится линия уровня  перпендикулярно градиенту (проще всего провести линию
перпендикулярно градиенту (проще всего провести линию 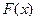 = 0).
= 0).
4) Опускаются перпендикуляры из всех вершин выпуклого множества на линию уровня, и определяется точка искомого экстремума целевой функции с учетом направления градиента. Решаются совместно уравнения, задающие прямые, на пересечении которых находится эта точка.
5) Определяется оптимальное решение 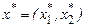 и экстремальные значения целевой функции
и экстремальные значения целевой функции 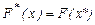 .
.
Задача. Фирма получила заказ на изготовление курток и пальто по моделям из материала заказчика. Расчет показал, что на изготовление куртки потребуется 3 усл. ед. материала, на пальто – 4 усл. ед., при ограничении имеющегося материала 170 усл. ед. Причем при пошиве куртки фирма располагает 2 станко-часами, пальто – 5 станко-часами, при ограничении 160 станко-часов. За пошив куртки заказчик платит 2 ден. ед., пальто – 4 ден. ед. Ассортимент заказчик не указывает. Найти число курток и пальто, которое фирма может предложить заказчику для получения максимальной прибыли.
Данные задачи можно представить в виде технологической таблицы:
| Ресурсы | Нормы расхода на единицу продукции | Объем ресурса | |
| Куртка | Пальто | ||
| Сырье, усл. ед. | |||
| Оборудование, станко-час | |||
| Прибыль от реализации ед. продукции, ден. ед. |
Решение задачи:
Введем обозначения: х1 - количество курток, х2 - количество пальто. Тогда математическая модель задачи примет вид:

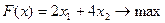 .
.
Для построения ОДР ЗЛП строим на плоскости  соответствующие данным ограничениям-неравенствам граничные прямые:
соответствующие данным ограничениям-неравенствам граничные прямые:
 ;
; 
| x1 | –10 | x1 | ||||
| x2 | x2 |
Находим полуплоскости, в которых выполняются данные неравенства. Для этого вследствие выпуклости любой полуплоскости достаточно взять произвольную точку, через которую не проходит соответствующая граничная прямая, и проверить, удовлетворяет ли эта пробная точка ограничению-неравенству. Если удовлетворяет, то данное неравенство выполняется в полуплоскости, содержащей пробную точку. В противном случае берется полуплоскость, не содержащая пробной точки. В качестве пробной точки часто удобно брать начало координат. Для нашей задачи ОДР – множество точек четырехугольника АВСО с учетом неотрицательности переменных  (рис. 2.3)
(рис. 2.3)
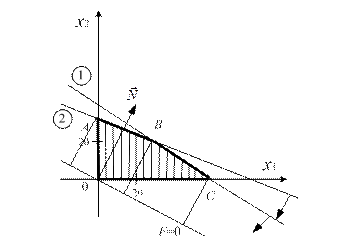
Рис. 2.3
Выпишем градиент  . Так как градиент необходим лишь для выяснения направления возрастания целевой функции, то в данном случае для большей наглядности удобно построить вектор
. Так как градиент необходим лишь для выяснения направления возрастания целевой функции, то в данном случае для большей наглядности удобно построить вектор  . Пусть
. Пусть  , тогда
, тогда  .
.
Проведем линию уровня 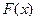 = 0, то есть
= 0, то есть

| x1 | –20 | |
| x2 |
Опустим перпендикуляры из угловых точек на линию уровня. С учетом направления градиента целевая функция достигает максимума в точке В, координаты которой можно найти, решив систему уравнений:

Решение системы x1 = 30, х2 = 20.
Так как x* = (30;20), то  .
.
Ответ: x* = (30;20),  .
.
Таким образом, для получения фирмой максимальной прибыли в размере 140 ден. ед. надо предложить заказчику пошить 30 курток и 20 пальто.
3. Возможные случаи области допустимых решений при решении ЗЛП графическим методом:
1) Единственное решение (рис. 2.4)

Рис. 2.4
2) Бесконечное множество решений (альтернативный оптимум (максимум), рис. 2.5)

Рис. 2.5
3) Неограниченность целевой функции сверху (рис. 2.6)

Рис. 2.6
4) Отсутствие оптимального решения (рис 2.7)

Рис. 2.7
5) ОДР – единственная точка, где целевая функция достигает одновременно и максимального и минимального значений (рис. 2.8)

Рис. 2.8
6) Пустое множество решений (рис. 2.9)

Рис. 2.9
4. Основные свойства решений ЗЛП:
1) Область решения ЗЛП, если она непуста, – выпуклое множество.
2) Основная теорема линейного программирования: Если ЗЛП разрешима, то целевая функция принимает экстремальное значение в одной из угловых точек или на одной из границ ОДР. В первом случае решение единственно, а во втором случае – бесконечное множество решений.
3) Если ОДР ограничена, непуста и целевая функция принимает экстремальное значение на одной из границ ОДР, то любое решение ЗЛП на этой границе является линейной комбинацией угловых точек, определяющих эту границу (рис. 2.10):
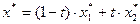 ,
,  .
.

Рис. 2.10
4) Если разрешимое ЗЛП включает n переменных и m ограничений, причем m < n, то в оптимальном решении отличными от нуля будут не более m переменных.
Дата добавления: 2014-12-03; просмотров: 562; Мы поможем в написании вашей работы!; Нарушение авторских прав |